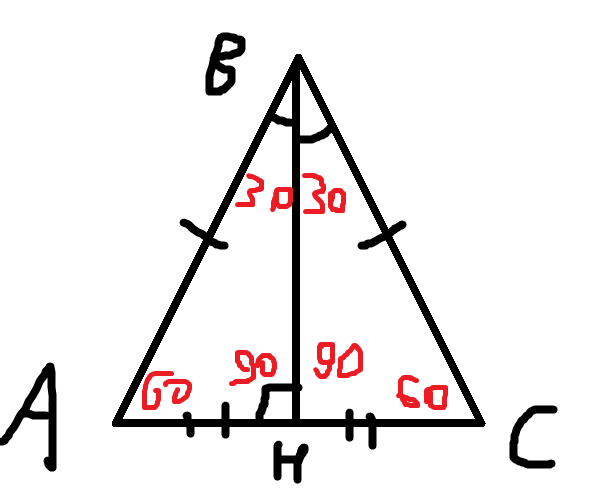
ПОМОГИТЕ ПОЖАЛУЙСТА!!! СРОЧНО!!!ЗАДАНИЕ1:Чему равны углы треугольника,на которые высота разбивает равносторонний треугольник?

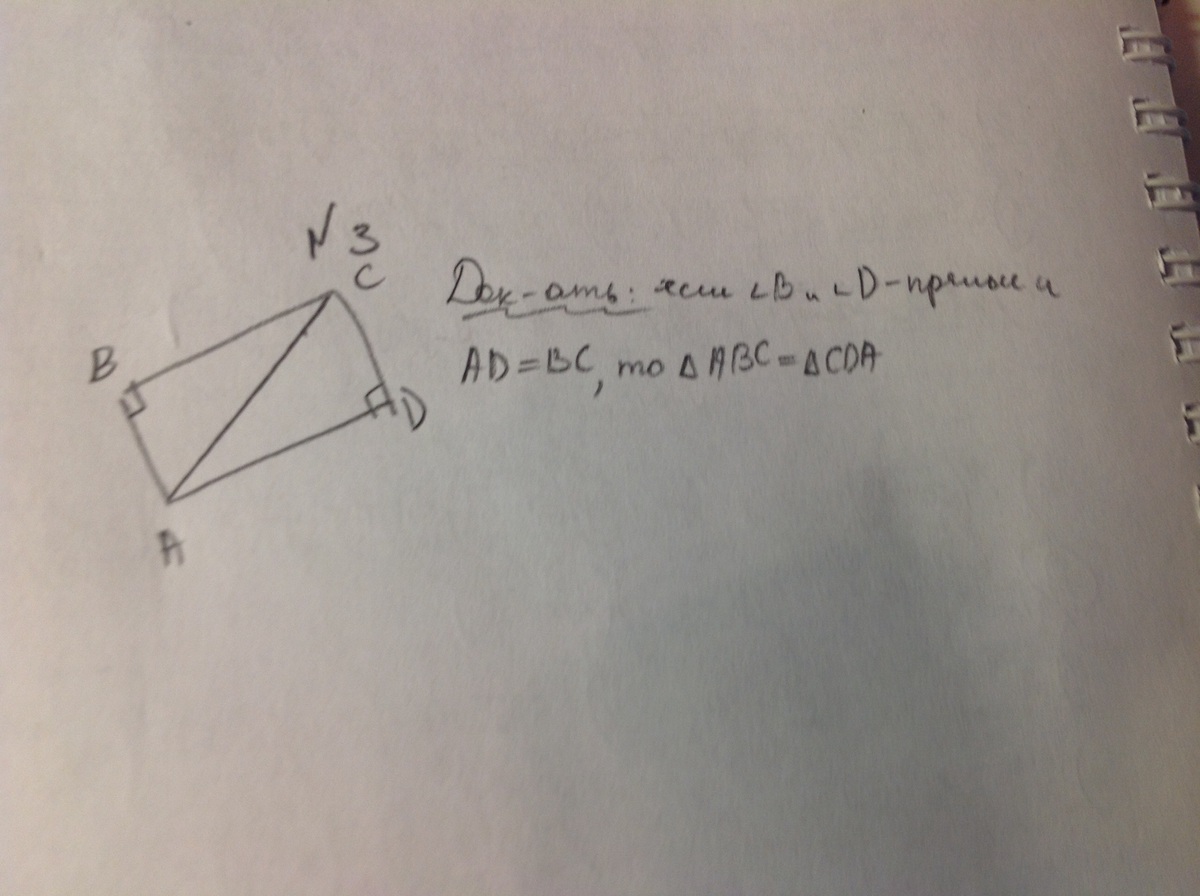
ЗАДАНИЕ2:ДОКАЗАТЬ,ЧТО ЕСЛИ УГОЛ Б и УГОЛ Д-ПРЯМЫЕ И АД=ВС,ТО ТРЕУГОЛЬНИК АВС=ТРЕУГОЛЬНИКУ СДАТЬ.

ЗАДАНИЕ3:НАЙТИ УГЛЫ ТРЕУГОЛЬНИКА ВОР,ЕСЛИ АВС-РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК,С ОСНОВАНИЕМ ВС,УГОЛ С=68 ГРАДУСОВ,ОР ПАРАЛЛЕЛЬНО АС.
ЗАДАНИЕ4:В ТРЕУГОЛЬНИКЕ СДЕ,СТОРОНЫ СЕ=ДЕ,БИССЕКТРИСЫ СМИ ДН ПЕРЕСЕКАЮТСЯ В ТОЧКЕ А. ДОКАЗАТЬ:ТРЕУГОЛЬНИК ДАМ=САН

РЕШИТЕ ХОТЬ ЧТО-ТО!!! ЗАРАНЕЕ ОГРОМНОЕ СПАСИБО!!!

. Т.к. в равностороннем треугольнике все углы равны по 60 градусов, то <ACB=<CAB=60градусов. Т.к. BH - высота, то <BHC=<BHA=90 градусов, а значит <ABH=<HBC=180-90-60=30 градусов каждый, это также можно объяснить тем, что в равностороннем треугольнике любая высота, также является биссектрисой и медианой.
Ответ: 90 градусов, 60 градусов и 30 градусов.
2. BC=AD, пусть BC=AD=x, тогда по теореме Пифагора: AC^2=AB^2+x^2=CD^2+x^2=>AB^2=CD^2=>AB=CD. Т.к. AB=CD, BC=AD, <ABC=<ADC=90градусов, то по 1-ому признаку равенства треугольников треугольники ABC и ACD равны.
Ответ: треугольники ABC и ACD равны.
3. Т.к. OP||AC, то <BPO=<PCA=68 как соответственные при секущей PC, а значит <OPB=<OBP=68 градусов (Т.к. BAC - равнобедренный с основанием BC). Т.к. сумма градусных мер всех углов любого треугольника равна 180, то <BOP=180-68-68=44 градуса.
Ответ: <OBP=<BPO=68 градусов; <BOP=44 градуса.
4. Т.к. CDE-равнобедренный(т.к. CE=DE), то <MCD=<CDN, а значит <CDN=<NDM=<DCM=<MCN. Отсюда следует, что треугольник CDA-равнобедренный, с основанием CD, тоесть CA=DA; далее, <DAM=<CAN как вертикальные. Итого: т.к. AD=AC, <DAM=<CAN, <NDM=<MCN, то по 2-ому признаку равенства равны треугольники DAM и CAN.
Ответ: треугольники DAM и CAN равны.