Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
1 сентября 2022 21:18
7585
Решите пожалуйста.Под буквой "б" объясните подробно...
А) 5cosx + 4/ 4tgx -3 =0
Б) [-4п; -5п/2 ]
1
ответ
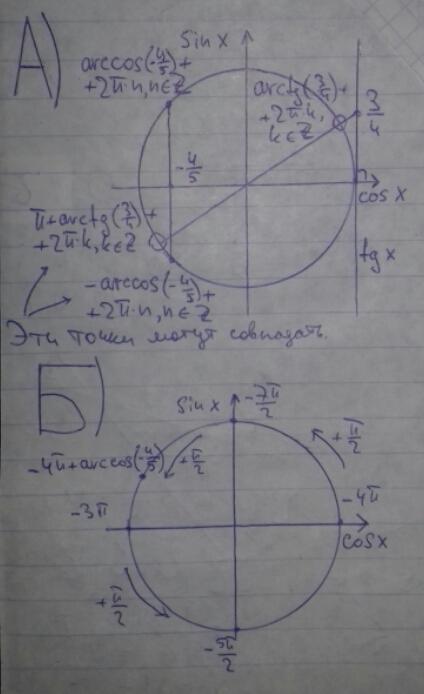
А)

Если , то для х ∈ 3ч. :
, то для х ∈ 3ч. :

Значит на тригонометрической окружности точки и
и  совпадают, поэтому решением системы будет
совпадают, поэтому решением системы будет 
Б)
На промежутке [0;2π] корнем системы будет:
Значит на промежутке [-4π;-2π] корень будет:
Заданный в условии промежуток не ограничивает корень системы на промежутке [-4π;-2π].
Ответ: А)
Б)
Если
Значит на тригонометрической окружности точки
Б)
На промежутке [0;2π] корнем системы будет:
Значит на промежутке [-4π;-2π] корень будет:
Заданный в условии промежуток не ограничивает корень системы на промежутке [-4π;-2π].
Ответ: А)
Б)
0
·
Хороший ответ
1 сентября 2022 21:18
Остались вопросы?
Еще вопросы по категории Алгебра
Решить уравнение : а) 2x-3(x-1)=4+2(x-1); б) x/3 + x+1/4 = 2...
Навстречу друг другу едут два поезда. Скорость первого поезда равна 60 км/ч , а скорость второго 50 км/ч. Длина первого поезда 350 м, а длина второго...
Решениеуравнения(cos 75 градусов+sin 75 граддусов)...
Картина имеет форму прямоугольника со сторонами 36 см и 50 см. Её вставили в раму так, что вокруг картины получилась окантовка одинаковой ширины. Площ...
вычислите определённый интеграл: а)интеграл (П/2;0) (-1/корень x+cos x)dx; б) интеграл (2;1) 2x^3+7x^2-3x-5/x^2*dx...