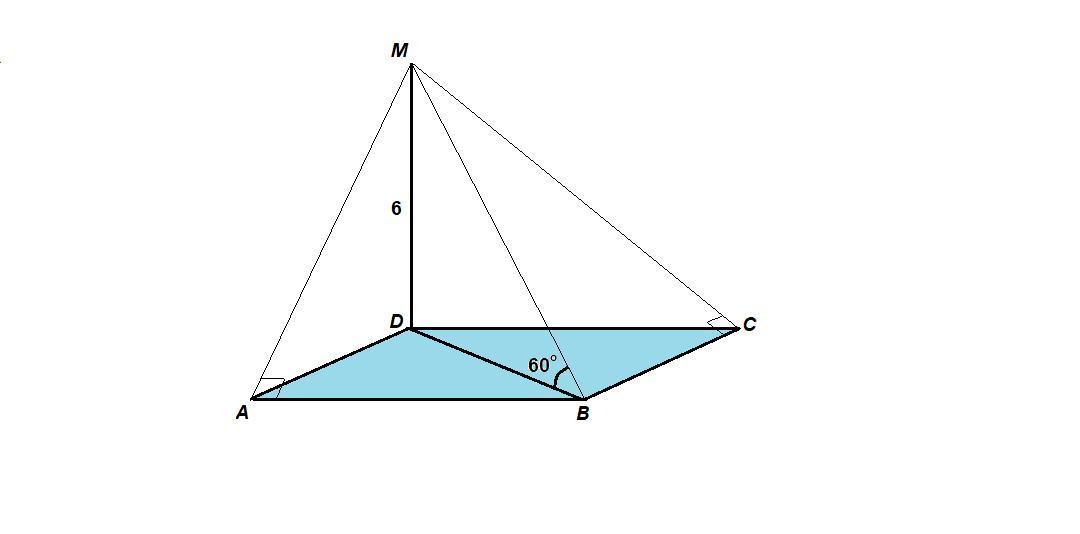
Из точки М проведен перпендикуляр МД, равный 6 см, плоскости квадрата АВСД. Наклонная МВ образует с плоскостью квадрата угол 60º. а) Док-ть, что треугольники МАВ и МСВ-прямоугольные; б) Найдите сторону квадрата; в) Найдите площадь треугольника АВД

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ:
б) √6 см
в) 3 см
Объяснение:
BD - проекция наклонной МВ на плоскость квадрата, значит
∠MBD = 60°.
а) AD⊥AB как стороны квадрата, AD - проекция МА на плоскость, значит МА⊥АВ по теореме о трех перпендикулярах, т.е.
ΔМАВ прямоугольный.
DC⊥BC как стороны квадрата, DC - проекция МС на плоскость, значит МС⊥ВС по теореме о трех перпендикулярах, т.е.
ΔМСВ прямоугольный.
б) Из прямоугольного треугольника MBD:
$tgMBD=\dfrac$
$BD=\dfrac=\dfrac=\dfrac{\sqrt}=2\sqrt$ см
BD = AB√2 как диагональ квадрата,
$AB=\dfrac{\sqrt}=\dfrac}{\sqrt}=\sqrt$ см
в) ΔABD прямоугольный, равнобедренный.
$S_=\dfracAB^=\dfrac\cdot 6=3$ см

Хороший ответ

5 апреля 2023 10:28

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Площадь параллелограмма ABCD равна 115. Точка Е - середина стороны AD. Найдите площадь треугольника ABE... В треугольнике ABC AC=BC=1, AB=корень из 3. Найдите угол C... Найти катеты прямоугольного треугольника , если гипотенуза равна 4 см , а один из углов 45 градусов... 17. Проектор полностью освещает экран A высотой 190 см, расположенный на расстоянии 210 см от проектора. На каком наименьшем расстоянии (в сантиметра... в прямом параллелепипеде стороны основания равны 3 см и 4 см, а угол между ними-60. Площадь боковой поверхности ровна 15√3 см². Найти объём параллелеп...