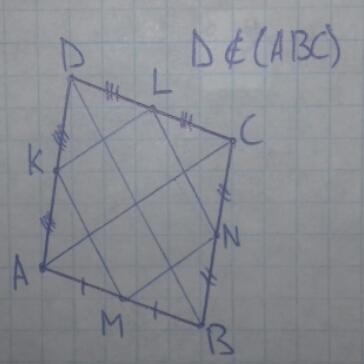
Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма

1 ответ

Посмотреть ответы

Megamozg

2205

M, N, L и K середины сторон AB, BC, CD и DA соответственно.
Отрезок соединяющий середины двух сторон в треугольнике является средней линией, которая параллельна третьей стороне.
MN, NL, LK и KM среднии линии в ΔABC, ΔBCD, ΔCDA и ΔDAB соответственно. Значит MN║AC; NL║BD; LK║CA=AC; KM║DB=BD.
MN║AC║LK ⇒ MN║LK - по транзитивности параллельных прямых а пространстве.
Так же NL║KM (NL║BD║KM).
В четырёхугольнике MNLK противоположные стороны параллельны (MN║LK и NL║KM), то есть это параллелограмм. А точки M, N, L и K его вершины. Доказано.

Хороший ответ

5 апреля 2023 10:54

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Как называется угол 360 градусов если 180градусов называется развернутый... Картинка имеет форму прямоугольника со сторонами 19 см и 32 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинак... Начертите неразвернутый угол AB отметьте две точки внутри этого угла 2 точки вне этого угла и две точки на сторонах угла...  В треугольнике 𝐴𝐵𝐶 медианы пересекаются в точке 𝑀. Через точку 𝑀 проведена прямая, параллельная стороне 𝐵𝐶 и пересекающая стороны 𝐴𝐵 и... Большая боковая сторона прямоугольной трапеции равна 12√2 см, а острый угол - 45°, найдите площадь трапеции, если известно, что в трапецию можно вписа...