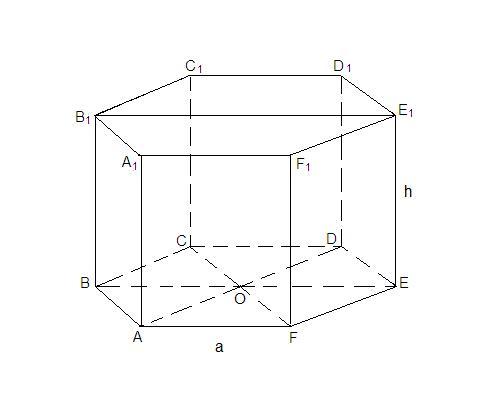
Площадь наибольшего диагонального сечения правильной шестиугольной призмы равна 10. Найдите площадь боковой поверхности этой призмы.

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ:
30 кв. ед.
Объяснение:
В основании правильной призмы - правильный шестиугольник.
Радиус окружности, описанной около правильного шестиугольника, равен его стороне.
Большая диагональ его - диаметр описанной окружности.
Пусть а - сторона основания, тогда
ВЕ = 2а
BB₁E₁E - большее диагональное сечение, прямоугольник.
$S_=BE\cdot EE_1=2ah=10$
Площадь боковой поверхности:
Sбок. = Pосн. · h = 6a · h = 3 · (2ah) = 3 · 10 = 30 кв. ед.

Хороший ответ

5 апреля 2023 11:11

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

1) Построить описанную окр-ть около тупоугольного треугольника 2) Построить вписанную окр-ть в остроугольный треугольник Желательно все на листе А4... Алюминиевый провод диаметром 4 мм имеет массу 6,8 кг. Найдите длину провода (плотность алюминия 2,6 г/см3)... Дана правильная треугольная призма, все ребра которой равны 8 сантиметров. Найдите площадь полной поверхности данной призмы.... Найти стороны прямоугольного треугольника , если меньший из его катетов на 18 см меньше гипотенузы , а разность катетов 17 см. Помогите пожалуйста!!... Напишите уравнение сферы с центром А, проходящей через точку N, если: А (-1;1;0). N (-2;2;1)....