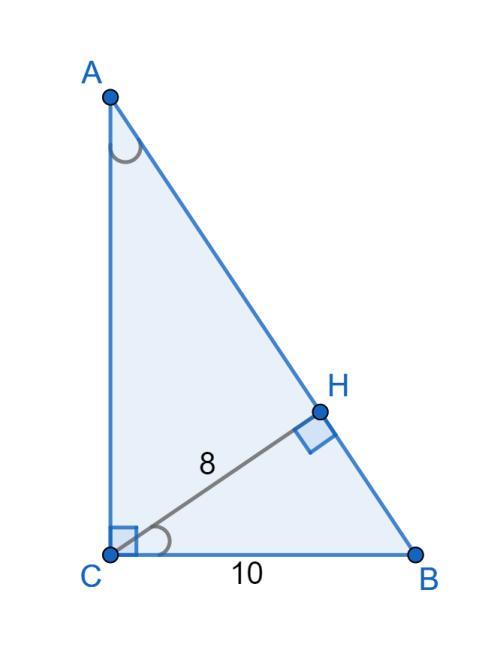
в треугольнике авс угол с равен 90 градусов, высота сн равна 8, катет вс равен 10. найдите тангенс угла а.

Ответ:
решение представлено на фото
Пошаговое объяснение:

Ответ:
tg∠A = 3/4
Пошаговое объяснение:
Рисунок прилагается.
Дано: ΔABC; ∠C = 90°; BC = 10; высота CH = 8.
Найти tg∠A.
Так как CH высота, то ∠CHB = 90° ⇒ ΔCHB прямоугольный (его гипотенуза CB = 10, катет CH = 8).
Из ΔCHB по т.Пифагора найдем катет BH.
BH = √(CB² - CH²) = √(10² - 8²) = √(100 - 64) = √36 = 6.
BH = 6.
ΔABC и ΔCHB подобны по двум углам: ∠B общий, ∠ACB = ∠CHB = 90° по условию. У подобных треугольников соответствующие углы равны.
⇒ ∠CAB = ∠BCH;
tg∠CAB = tg∠BCH = BH / CH = 6/8 = 3/4 (тангенс в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему катету).
tg∠A = 3/4.