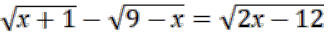Помогите решить(√x+1)-(√9-x)=(√2x-12)

Так как выражение под знаком корня не может быть отрицательным, то отсюда следуют неравенства:

x+1>=0;

9-x>=0;

2*x-12>=0

Решая их, находим x>=-1; x<=9; x>=6. Объединяя эти решения, получаем область допустимых значений (ОДЗ) переменной x: 6<=x<=9.

Возведём обе части уравнения в квадрат. Получим:

x+1-2*sqrt[x+1)*(9-x)]+9-x=2*x-12, где sqrt [ ] - квадратный корень из выражения, находящегося в скобках [ ].

После приведения подобных членов это уравнения перепишется так:

2*sqrt[(x+1)*(9-x)]=22-2*x. Сократив обе части на 2, получим:

sqrt[(x+1)*(9-x)]=11-x. Возводя обе части в квадрат, получаем:

(x+1)*(9-x)=(11-x)^2. После раскрытия скобок и приведения подобных членов приходим к квадратному уравнению:

2*x^2-30*x+112=0, или - после сокращения на 2 - к равносильному уравнению:

x^2-15*x+56=0. Оно имеет корни x1=8, x2=7. Оба корня принадлежат ОДЗ. Подставляя их в исходное уравнение, убеждаемся, что они ему удовлетворяют:

sqrt[8+1]-sqrt[9-8]=3-1=2=sqrt[2*8-12]; sqrt[7+1]=2*sqrt[2]; 2*sqrt[2]-sqrt[2]=strt[2].

Ответ: x1=8, x2=7.