Срочно
Установите соответствие между функциями (1-3) и производными (А-Г) этих функций.

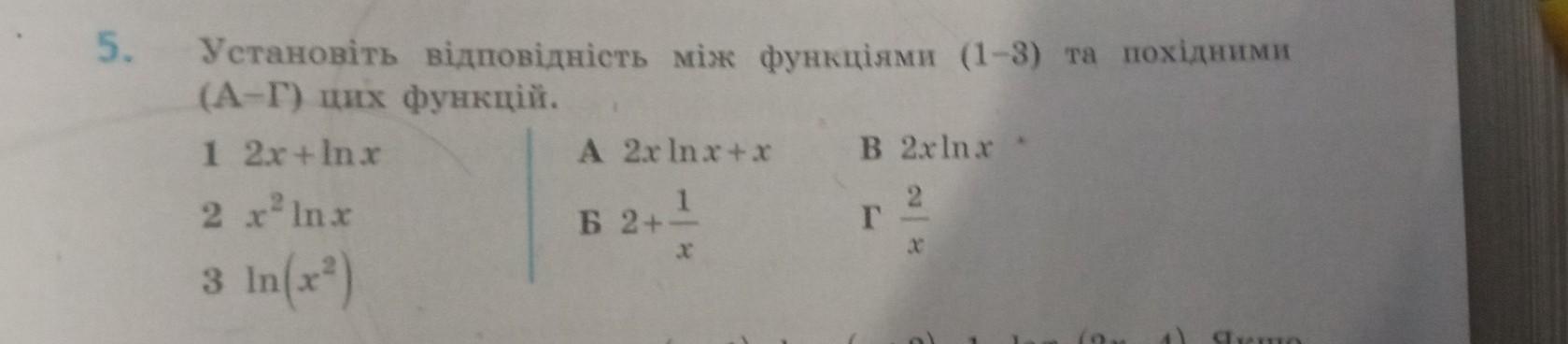
1 ответ

Посмотреть ответы

v.petrogradov

Ответ:

1Б: производная функции y=2x+ln x это y'=2+1/x.
2A: производная функции y=x²ln x это y'=2xln x+x.
3Г: производная функции y=ln(x²) это y'=2/x.

Пошаговое объяснение:

Правила нахождения производных, которые нам понадобятся:
$\large \boldsymbol {} \displaystyle \begin{|c|c|c|c|c|c|c|}\cline f(x)&f(x)\pm g(x)&f\big(g(x)\big)&uv&\ln x&x^n&x\cline f'(x)& f'(x)\pm g'(x)&f'(x)\cdot g'(x)&uv'+v'u&\frac &nx^&1 \cline \end$

Используя вышеуказанную таблицу, находим производные функций.

1) y=2x+ln x
$\displaystyle y'=(2x+\ln x)'=(2x)'+(\ln x)' = 2\cdot1+\frac=2+\frac$
1Б: производная функции y=2x+ln x это y'=2+1/x.

2) y=x²ln x
$\displaystyle y'=(x^2\ln x)' = (x^2)'\ln x+(\ln x)'x^2= 2x\cdot\ln x+\frac{\not x}\cdot \not \!x^2= 2x\ln x+x$
2A: производная функции y=x²ln x это y'=2xln x+x.

3) y=ln(x²)
$\displaystyle y'=\big(\ln (x^2)\big)' = \frac\cdot (x^2)'= \frac{\not \!x^2} \cdot 2\!\!\!\!\not x = \frac$
3Г: производная функции y=ln(x²) это y'=2/x.

Хороший ответ

11 ноября 2022 11:13

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Как можно упростить выражение 1 cos 2a?... для варенья из малины на 2 части ягод берут 3 части сахара.1)Сколько сахара надо взять на 2 кг 600 гр ягод?2)Сколько кг малины было у мамы, если для в... Какие виды массажа бывают?... На рисунке изображены графики функций y=5-x^2 и y=4x Вычислите абсциссу точки B... Какие числа указаны в задании?...

СрочноУстановите соответствие между функциями (1-3) и производными (А-Г) этих функций.​

Ответ:

Пошаговое объяснение:

Срочно
Установите соответствие между функциями (1-3) и производными (А-Г) этих функций.