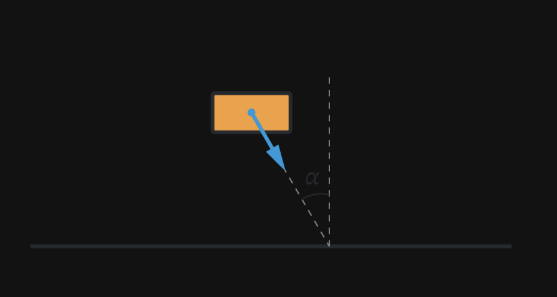
Цилиндрическая шайба массой m=200

 г скользит, не вращаясь, со скоростью v0=2

 м/с по гладкому горизонтальному льду таким образом, что её основания вертикальны и параллельны неподвижному вертикальному борту, с которым эта шайба сталкивается. Угол падения (угол между линией движения центра масс шайбы и перпендикуляром к борту) равен α=30∘. Известно, что нормальные деформации борта являются упругими (при α=0

 удар был бы упругим), но между бортом и основанием шайбы есть трение, и коэффициент трения равен μ=0,3. 

1)Найдите угол отражения шайбы. Ответ запишите в градусах, округлив до десятых.

2)Определите количество теплоты, которое выделится из-за трения шайбы о борт во время удара. Ответ запишите в Дж, округлив до сотых.

Условие задачи можно упростить, если ввести координатную систему, где ось x направлена вдоль нормали к борту (то есть перпендикулярно к нему), а ось y – вдоль борта (касательная к нему). Тогда при столкновении шайба имеет начальную скорость

  v₀ = (vₓ₀, vᵧ₀) = (2·cos 30°, 2·sin 30°) = (√3, 1) м/с   (√3 ≈ 1.732)

При отсутствии трения (и с упругим нормальным взаимодействием) при столкновении нормальная (x‑) составляющая скорости меняется на противоположную, а касательная (y‑) остаётся неизменной: получилась бы скорость (–√3, 1). Однако между бортом и шайбой действует трение с коэффициентом μ = 0.3, которое действует вдоль направления y (касательно к поверхности контакта) и изменяет касательную составляющую.

Ниже приводится подробное решение задачи.

─────────────────────────────
1) Определение угла отражения

Поскольку контакт происходит с «упругим» нормальным откликом, изменение импульса в направлении x определяется исключительно необходимым изменением для реверса vₓ, т.е. 

  Δpₓ = m (vₓ,final – vₓ,initial) = m (–√3 – √3) = –2m√3.

Под модулем нормальный импульс (по оси x) равен

  Jₙ = 2 m √3 = 2·0.2·√3 = 0.4√3 (кг·м/с).

При наличии трения на протяжении удара действует контактная сила, величина которой в каждой мгновенной точке равна μ N, где N – нормальная сила. При быстром ударе соотношение интегральных импульсов сохраняется – касательный (трением создаваемый) импульс равен

  Jₜ = μ Jₙ = μ·(0.4√3) = 0.4μ√3.

Важно правильно определить знак. Изначально касательная скорость vᵧ₀ = +1 м/с. Так как появляется относительное скольжение в направлении положительного y, сила трения всегда направлена против этого движения, то есть действует со знаком «минус». Значит изменение импульса по y:

  Δpᵧ = –0.4μ√3.

Отсюда итоговая касательная составляющая скорости будет

  vᵧ,final = vᵧ,initial + (Δpᵧ/m) = 1 – (0.4μ√3 / 0.2) = 1 – 2μ√3.

Подставляем μ = 0.3 и √3 ≈ 1.732:

  2μ√3 = 2·0.3·1.732 = 1.0392,

  vᵧ,final ≈ 1 – 1.0392 = –0.0392 м/с.

То есть после удара по оси x скорость станет vₓ,final = –√3 ≈ –1.732 м/с (смена направления в нормали), а по оси y почти нулевая, но с малым отрицательным значением (означает, что направление стало чуть «вниз» вдоль борта, если принять первоначальное направление y как «вверх»).

Определим угол отражения α′ как угол между направлением скорости и нормалью к борту (осью x). Так как по модулю vₓ,final ≈ 1.732, а |vᵧ,final| ≈ 0.0392, то

  tan(α′) = |vᵧ,final| / |vₓ,final| ≈ 0.0392 / 1.732 ≈ 0.0226,
  α′ ≈ arctan(0.0226) ≈ 1.3°.

Ответ по первому пункту: угол отражения относительно нормали ≈ 1.3° (при этом следует отметить, что отражённая траектория имеет почти чисто горизонтальное направление, противоположное начальному нормальному движению).

─────────────────────────────
2) Определение количества теплоты, выделившегося из-за трения

Энергия теряется только за счёт работы силы трения. Можно найти разницу между начальной и конечной кинетической энергией.

Начальная кинетическая энергия:
  E₀ = ½ m v₀² = ½ · 0.2 · (2)² = 0.4 Дж.

Найдем конечную скорость. После удара по координатам имеем:
  vₓ,final = 1.732 м/с (по модулю), vᵧ,final ≈ –0.0392 м/с.
Тогда
  v_final = √(vₓ,final² + vᵧ,final²) ≈ √( (1.732)² + (0.0392)² )
               = √(3 + 0.001537) ≈ √(3.00154) ≈ 1.732 m/с.
Заметим, что позже потеря энергии невелика.

Конечная кинетическая энергия:
  E_final = ½ m v_final² ≈ ½ · 0.2 · (3.00154) = 0.100·3.00154 ≈ 0.30015 Дж.

Таким образом, потеря энергии (которая перейдёт в тепло) равна:

  ΔE = E₀ – E_final ≈ 0.4 – 0.30015 = 0.09985 ≈ 0.10 Дж.

─────────────────────────────
Ответы:

1) Угол отражения (относительно нормали к борту) равен примерно 1.3°.

2) Количество теплоты, выделившееся за счет трения, составляет примерно 0.10 Дж.

Эти результаты получены при предположении, что во время удара скольжение сохраняется, и сила трения на протяжении контакта оказывается равна μ N, интегральный импульс трения равен μ умноженному на интегральный нормальный импульс.