- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
В лесу на разных кустах висят 100 шнурков. Сова говорит, что в среднем 3 шнурка из 4 ей не подходят. Ив утверждает, что ему не подходит 4 шнурка из 5( в среднем). Оба правы. Сколько шнурков не подходят ни Сове, ни Иа? Найди наименьшее возможное число.
Дано:
Всего шнурков 100;
число шнурков, неподходящих Сове равно 3/5 от общего числа;
число шнурков, неподходящих Иа равно 4/5 от общего числа.
Найти: минимальное число шнурков, одновременно неподходящих Иа и Сове
Решение
Пусть А - число шнурков, неподходящих Иа,
В - число шнурков, неподходящих Сове,
С - число шнурков, одновременно неподходящих Иа и Сове,
тогда
А=100*4/5=80
В=100*3/5=75
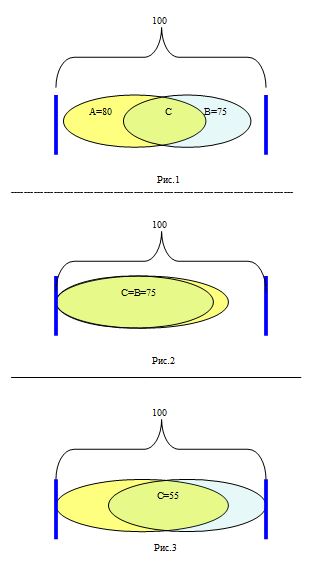
Число шнурков для выбора (см.рис.1) ограничено количеством 100,
т.е. если Сове не подходят 75 из 100, то Иа не подойдут 80 из тех же 100.
Это означает, что среди числа шнурков А, неподходящих Иа, будет какое-то количество шнурков В, неподходящих Сове.
На рис.2 представлен вариант, когда все шнурки, неподходящие для Совы, не подходят также для Иа.
На рис.3 представлен вариант, когда число шнурков, которые одновременно
не подходят Иа и Сове, минимально.
В общем случае:
А+В-С ≤100
Отсюда
С≥55
Следовательно, минимальное число шнурков, одновременно неподходящих Иа и Сове, С=55
Ответ: 55
Решение.
Рассмотрим три возможных варианта решения задачи.
Первый вариант
1. Сове не подходят 3/4 шнурков 100×3/4=75
2. Сове подходят
100-75=25
3. Иа не подходят 4/5 шнурков
100×4/5=80
4. Иа подходят
100-80= 20 шнурков
5. Возьмём 75 шнурков, которые не подходят Сове
Среди них наибольшее число подходящих Иа - это 20 шнурков, остальные 75-20=55 шнурков Иа не подойдут и Сове тоже (взяли её шнурки)
Ответ: 55 шнурков не подойдут никому
Второй вариант
Первые 4 пункта решения те же, как в первом варианте
5. Возьмём 80 шнурков, которые не подойдут Иа, среди них наибольшее число подходящих Сове 25, остальные не подойдут Сове, 80-25=55 шнурков не подойдут Сове и Иа (взяли его шнурки)
Ответ: наименьшее число 55 шнурков никому не подойдут
Третий вариант
Первые 4 пункта решения задачи те же, как в первом варианте
5. Зная, что Сове подходят 25 шнурков, а ослику Иа подходят 20 шнурков из имеющихся в лесу 100 шнурков, видим, что наименьшее количество шнурков, которые подходят одновременно Сове и ослику Иа равно 20 (когда из 25 шнурков, подходящих Сове, 20 шнурков одновременно подходят ослику), а наибольшее количество шнурков, которые подходят одновременно Сове и ослику Иа равно 20+25=45 (когда из 25 шнурков, которые подходят Сове, ни один не подходит ослику Иа)
6. Зная, что наибольшее количество шнурков, которые одновременно подходят и Сове и ослику Иа равно 45, а всего шнурков 100, найдём количество шнурков, которые не подходят никому (это и есть минимальное количество шнурков, не подходящих ни Сове, ни ослику Иа)
100-45=55
Ответ: минимальное количество шнурков, которые не подходят никому, равно 55.

Дано
100 шнурков
Сове не подходят 4 из 4 шнурков
Та не подходят 4 из 5 шнурков
Найти наименьшее количество шнурков, которые не подходят никому
Решение
1. Сове не подходят 3/4 шнурков 100?3/4=75
2. Сове подходят
100-75=25
3. Иа не подходят
4/5 шнурков
100?4/5=80
4. Иа подходят
100-80= 20 шнурков
Возьмём 75 шнурков, которые не подходят Сове
Среди них максимум подходящих Иа - это 20 шнурков, остальные 75-20=55 шнурков Иа не подойдут и Сове тоже (взяли её шнурки)
Ответ: 55 шнурков не подойдут никому
Сова сообщает, что ей не подходят 3 из 4 шнурков, то есть количество шнурков, неподходящих Сове, равно ¾ от 100, то есть 75.
Иа говорит, что ему не подходит 4 из 5 шнурков, значит неподходящих для Иа — 4/5 от 100, то есть 80.
Обозначим A – множество шнурков, которые не подходят Сове (|A| = 75), и B – множество шнурков, неподходящих Иа (|B| = 80).
Нужно найти минимально возможное количество шнурков, которые не подходят ни Сове, ни Иа, то есть |A ∩ B|.
Применим принцип включения-исключения:
|A ∪ B| = |A| + |B| – |A ∩ B|.
При этом общее число шнурков не может превышать 100, то есть |A ∪ B| ≤ 100. Отсюда получаем:
75 + 80 – |A ∩ B| ≤ 100
155 – |A ∩ B| ≤ 100
|A ∩ B| ≥ 155 – 100 = 55.
Таким образом, минимально возможное количество шнурков, которые не подходят ни Сове, ни Иа, равно 55.