Для треугольника ABC известно следующее: AB=2√3, BC=8, ∠ABC=150∘. Найдите R^2, где R — радиус наименьшего круга, в который можно поместить этот треугольник. Срочно помогите, пожалуйста!!!

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ:
124
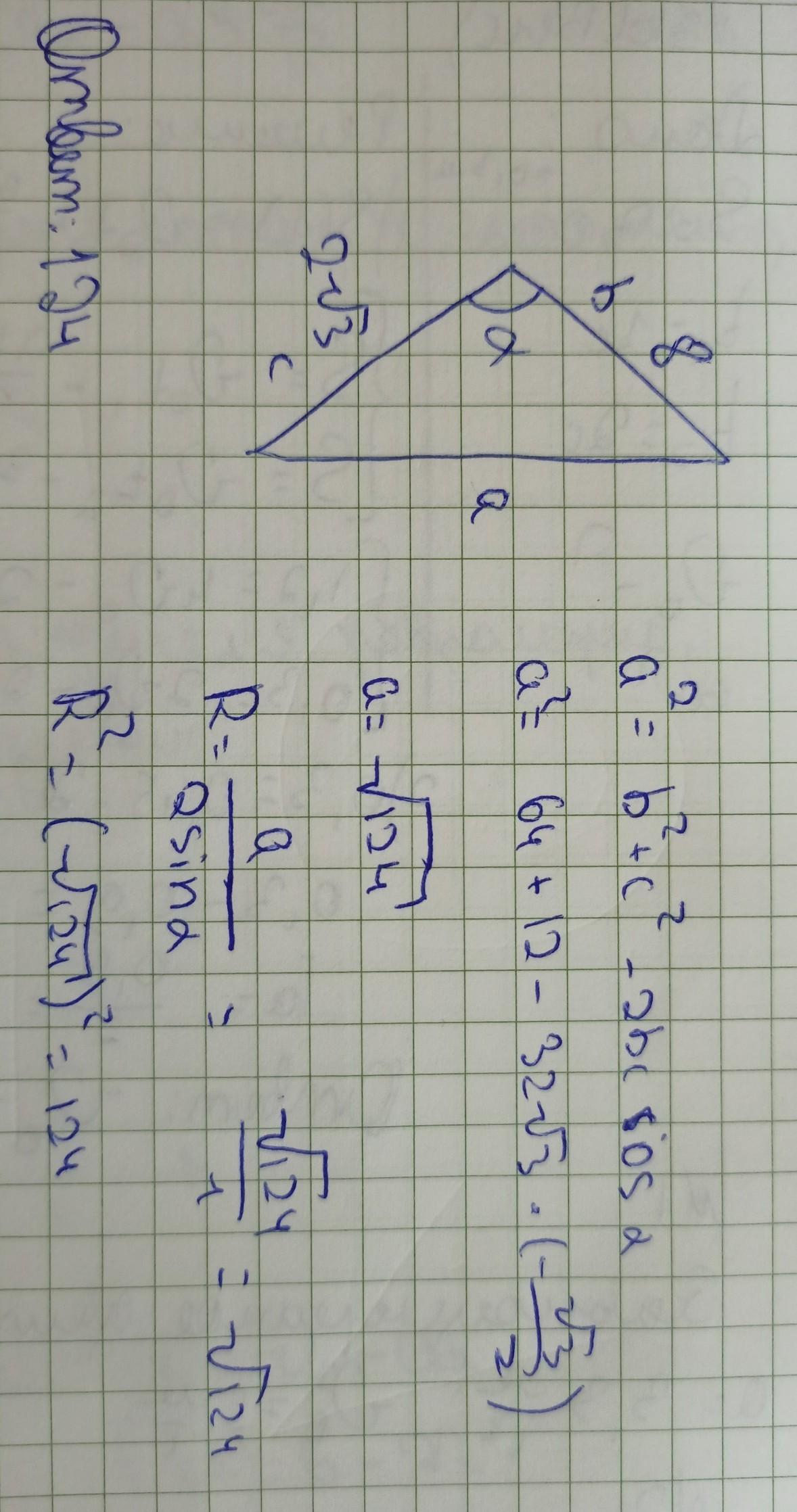
Решение на листке:
альфа = 150° ( синус 150 = 0.5 => 2*sin150 = 1 )
косинус 150° = (-✓3/2)
сначала находим сторону по теореме косинусов,
потом уже радиус через формулу описания

Хороший ответ

2 декабря 2022 02:51

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Из одного города в другой, расстояние между которыми равно 240 км, выехали одновременно автобус и автомобиль.Автобус двигался со скоростью на 20км/ч м... Какое число соответствует выражению '10 в минус 24 степени'?... Найдите отношения 12м : 6мм 12/6=... Какие значения могут принимать мнимые числа?... Объяснить значение фразеологизмов: Авгиевы конюшни, троянский конь, ахиллесова пята, гордиев узел, гомерический хохот (очень коротко)...