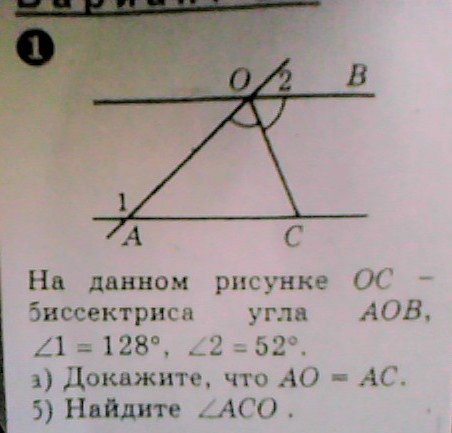
На данном рисунке ОС - биссектриса угла АОВ, угол1= 128 градусам, а угол2= 52 градусам. а) докажите, что АО = ОС б) Найдите угол АСО

2 ответа

Посмотреть ответы

DevAdmin

1720

угол AOC = углу COB = (180-52)/2 = 64
угол OAC = 180-128 = 52
угол ACO = 180-52-64 = 64
угол AOC = углу ACO = 64 ⇒ тр. AOC равнобед., а значит AO=AC

Хороший ответ

2 декабря 2022 02:52

Megamozg

2205

Угол ОАС = 52 градуса
Угол АОВ = 128 грудуса
Угол АОС = 128/2 = 64 градуса
Угол АСО = 180-(52+64) = 64 граудуса
Треугольник АОС: АС=АО потому, что углы при основании ОС равны(64=64) Следовательно - треугольник равнобёдренный и по этому АС=АО.

С тебя благодарность и "Лучший ответ" :D

2 декабря 2022 02:52

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

четырёхугольник ABCD вписан в окружность. Угол ABC равен 112 градусам, угол CAD равен 70 градусам. Найдите угол ABD. Ответ дайте в градусах... Вычислите: cos 60°+ tg 45°... Правильная шестиугольная пирамида , высота которой равна 35см , а сторона основания 5 см, пересечена плоскостью , параллельной основанию . Найти расст... Докажите, что отрезок, соединяющий середины оснований трапеции, делит её на две равные по площади части.... По краю юбки-солнце нужно пришить кружево. Сколько сантиметров кружева необходимо купить, если радиус круга, из которого шьют юбку, равен 50 см?...