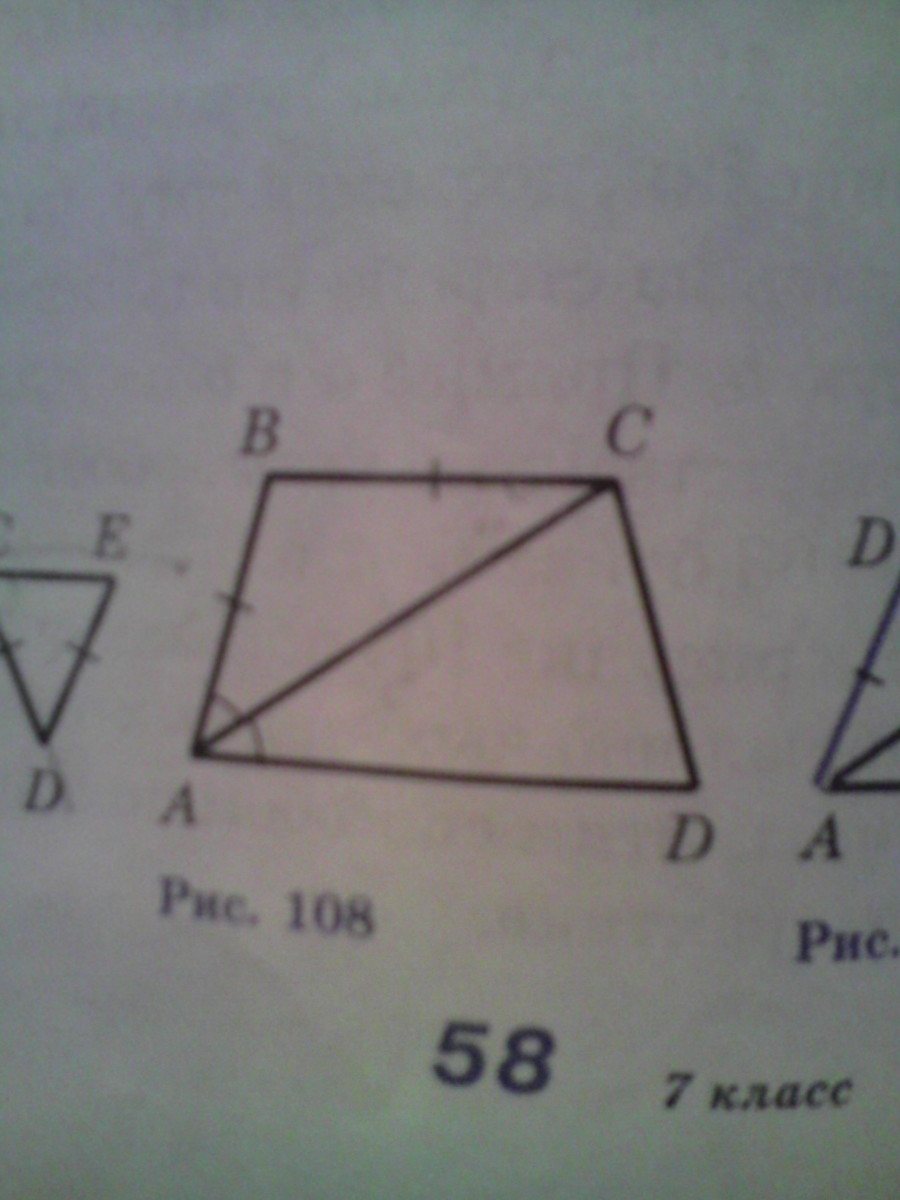
Используя данные рисунка 108, докажите, что BC||AD.

2 ответа

Посмотреть ответы

DevAdmin

1695

Треугольник АВС равнобедренный, следовательно углы при основании равны, т.е. угол ВАС=углу ВСА.
Из этого следует что углы САД и ВСА равны как накрест лежащие при параллельных прямых ВС и АД

Хороший ответ

2 декабря 2022 03:59

DevAdmin

1695

Треугольник АВС - равнобедренный, значит, угол ВАС=АСВ
Получается, что углы САД и ВСА - равные, значит, они являются накрест лежащие при параллельных прямых ВС и АД и секущей АС => ВС||АД

2 декабря 2022 03:59

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Какое значение будет иметь выражение 1 sin альфа cos альфа ctg альфа, если cos альфа = 0?... Памогло спасибо :) :):):):):):):) :):):):):):)... Решите уравнение cosX=корень из 3\2... Какое число находится на месте x?... Найдите сумму и разность чисел 60 и 40 50 и 30 40 и 20...