Образующая конуса, равная 12 см, наклонена к плоскости основания под углом 30 градусов. Найдите объем конуса

1 ответ

Посмотреть ответы

Megamozg

2205

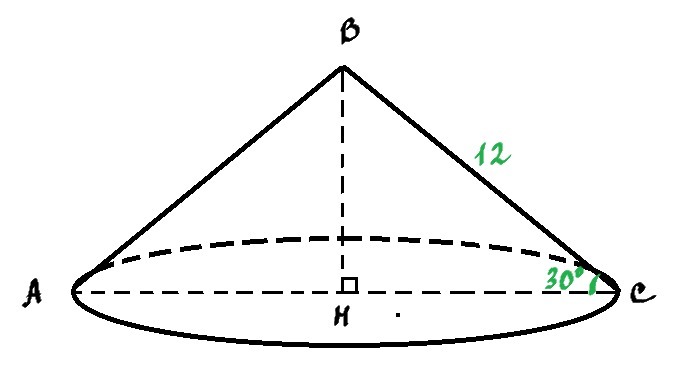
Рисунок прикреплен.

Дано: конус, ВС=12 см, ∠НСВ=30°

Найти: объем конуса

Решение: по условию образующая конуса наклонена к плоскости под углом в 30°. Это значит, что угол между образующей и радиусом основания конуса 30°.

Из вершины конуса опустим высоту. Обозначим её ВН.
ΔВНС прямоугольный.
У него известна гипотенуза ВС=12 и ∠НСВ=30°.

В прямоугольном треугольнике катет, лежащий напротив угла в 30° в два раза меньше гипотенузы.
$BH=\frac=\frac=6$

По теореме Пифагора найдем второй катет ΔВНС. Он же является радиусом основания конуса.

$HC=\sqrt=\sqrt=\sqrt=\sqrt$

Объем конуса вычисляется по формуле: $V=\frac\pi R^2h$ , где R - радиус основания, h - высота конуса.

$V=\frac\pi R^2h=\frac\pi (\sqrt)^2*6 =108*2\pi =216\pi$

Ответ: 216π см³

Хороший ответ

2 декабря 2022 05:10

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Сумма положительных чисел а и в равна 50. при каких значениях а и в их произведение будет наибольшим?... Какое число получится, если сложить 1 и 8, а затем записать результат в виде дроби?... Коля стёр некоторые цифры в примере на доске и написал вместо них буквы. Вместо одинаковых цифр он написал одинаковые буквы, а вместо разных цифр-разн... Выпишите все видимые грани параллелепипеда... В школьной библиотеке 1800 книг. Из них 28% составляют научно-популярные книги,43% произведения зарубежных писателей,а остальное - книги русских автор...