основание пирамиды является треугольник со сторонами 12 см 10 см 10 см. каждая боковая грань наклоненена к плоскости основании под углом 45 градусов. найти площадь полной поверхности .

1 ответ

Посмотреть ответы

DevAdmin

1720

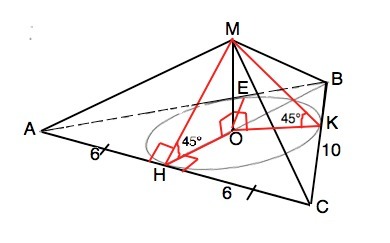
Если все грани пирамиды наклонены к плоскости основания под одним углом, то проекции высот этих граней равны радиусу вписанной в основание пирамиды окружности
ОН=ОК=ОЕ=r и, следовательно, высоты всех боковых граней равны.
r=2S (ABC):P
P=12+2•10=32
S=BH•AC:2=8•12:2=48 см²
2Ѕ=96 см²
∆ ABC - равнобедренный, его высота - медиана.
АН=СН=6 см
По т.Пифагора высота равнобедренного треугольника
ВH=√(ВС²-СН²)=√(100-36)=8 см
r=8•12:32=3 см
ВН⊥АС,
МН по т. о 3-х перпендикулярах перпендикулярен АС и является высотой боковой грани МАС.
МК=МН.
Из прямоугольного ∆ МОН отрезок МН=ОН:cosМНО=3:√2/2=3√2
S(бок)=МН•Р:2=48√2
S (полн)=Ѕ (АВС)+Ѕ(бок)=48+48√2=48(1+√2) см²

Хороший ответ

8 декабря 2022 13:30

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найдите углы равнобокой трапеции если один из её углов на 30 градусов больше второго... Сочинение на тему зачем нужна геометрия... Найдите площадь ромба изображённого на рисунке!... Образующая конуса составляет с плоскостью основания угол 45 градусов. Найдите объём конуса, если его высота равна 6 см.... Чему равна площадь прямоугольной трапеции, изображённой на рисунке?...