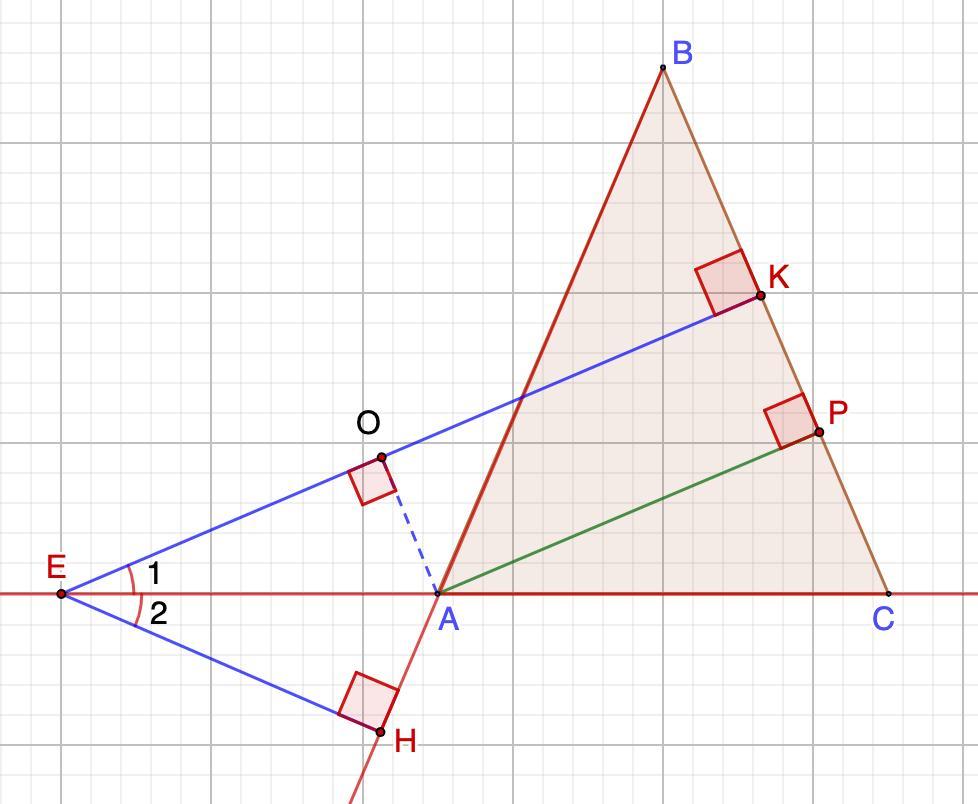
На прямой, содержащей основание равнобедренного треугольника, взята точка. Расстояния от этой точки до прямых, содержащих боковые стороны этого треугольника, различаются на 8 см. Чему равна высота этого треугольника, проведённая к любой боковой стороне?

Ответ:

Высота данного равнобедренного треугольника, проведённая к боковой стороне равна 8 см.

Объяснение:

Определить, чему равна высота данного равнобедренного треугольника, проведённая к любой боковой стороне?

Дано: ΔАВС - равнобедренный;

ЕК ⊥ ВС; ЕН ⊥ АВ.

ЕК - ЕН = 8 см.

АР - высота.

Найти: АР.

Решение:

Проведем АО ⊥ ЕК.

1. Рассмотрим ΔАВС - равнобедренный.

Углы при основании равнобедренного треугольника равны.
⇒ ∠С = ∠ВАС.


2. Рассмотрим ΔЕКС - прямоугольный.

Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠1 = 90° - ∠С

3. Рассмотрим ΔНЕА - прямоугольный.

Вертикальные углы равны.
⇒ ∠ЕАН = ∠ВАС (вертикальные)

∠2 = 90° - ∠ЕАН

3. Рассмотрим ΔЕОА и ΔЕАН - прямоугольные.

∠1 = 90° - ∠С

∠2 = 90° - ∠ЕАН

∠С = ∠ВАС (п.1)

∠ЕАН = ∠ВАС (п.2)

⇒ ∠1 = ∠2

ЕА - общая

⇒ ΔЕОА = ΔЕАН (по гипотенузе и острому углу)

В равных треугольниках против равных углов лежат равные стороны.
⇒ ЕН = ЕО.

4. ЕК - ЕН = 8 см (по условию)

или ЕК - ЕО = 8 см


5. Рассмотрим АОКР.

Если две прямые перпендикулярны третьей, то они параллельны между собой.
⇒ АО || КР; ОК || AP.

АОКР - параллелограмм.

Противоположные стороны параллелограмма равны.
⇒ ОК = AP = 8 см.

Ответ:
Высота данного равнобедренного треугольника, проведённая к боковой стороне равна 8 см.

Объяснение:
Определить, чему равна высота данного равнобедренного треугольника, проведённая к любой боковой стороне?

Дано: ΔАВС - равнобедренный;
ЕК ⊥ ВС; ЕН ⊥ АВ.
ЕК - ЕН = 8 см.
АР - высота.
Найти: АР.
Решение:
Проведем АО ⊥ ЕК.
1. Рассмотрим ΔАВС - равнобедренный.

• Углы при основании равнобедренного треугольника равны.

⇒ ∠С = ∠ВАС.

2. Рассмотрим ΔЕКС - прямоугольный.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠1 = 90° - ∠С

3. Рассмотрим ΔНЕА - прямоугольный.

• Вертикальные углы равны.

⇒ ∠ЕАН = ∠ВАС (вертикальные)
∠2 = 90° - ∠ЕАН

3. Рассмотрим ΔЕОА и ΔЕАН - прямоугольные.
∠1 = 90° - ∠С
∠2 = 90° - ∠ЕАН
∠С = ∠ВАС (п.1)
∠ЕАН = ∠ВАС (п.2)
⇒ ∠1 = ∠2
ЕА - общая
⇒ ΔЕОА = ΔЕАН (по гипотенузе и острому углу)

• В равных треугольниках против равных углов лежат равные стороны.

⇒ ЕН = ЕО.

4. ЕК - ЕН = 8 см (по условию)
или ЕК - ЕО = 8 см

5. Рассмотрим АОКР.

• Если две прямые перпендикулярны третьей, то они параллельны между собой.

⇒ АО || КР; ОК || AP.
АОКР - параллелограмм.

• Противоположные стороны параллелограмма равны.

⇒ ОК = AP = 8 см.