Докажите, что в треугольнике медиана не меньше высоты, проведенной из той же вершины

1 ответ

Посмотреть ответы

DevAdmin

1720

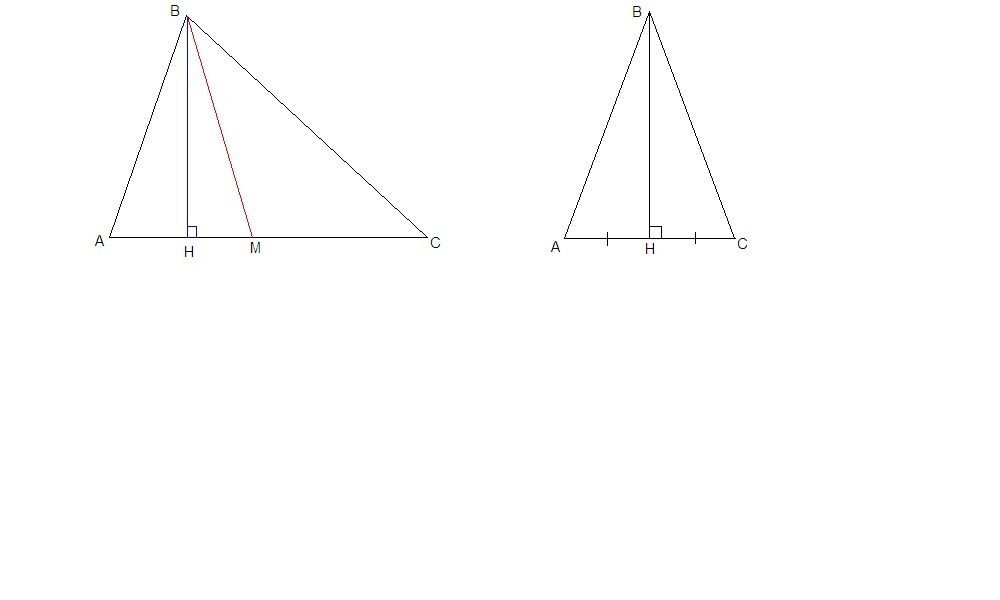
Медиана и высота, проведенные из одной вершины, образуют прямоугольный треугольник, в котором высота - катет, медиана - гипотенуза.
Гипотенуза всегда больше катета, поэтому медиана больше высоты.
Исключение составляет равнобедренный треугольник, в котором высота и медиана, проведенные к основанию, совпадают, значит равны.
Поэтому медиана не меньше высоты, проведенной из той же вершины.

Хороший ответ

8 декабря 2022 19:38

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Сформулируйте и докажите теорему о вычислении площади параллелограмма.... на стороне ac треугольника abc отмечена точка d так, что ad=9, dc=3.площадь треугольника abc=60.найдите площадь треугольника bcd... Как сделать пирамиду (геометрическая фигура) из бумаги БЕЗ КЛЕЯ?... Что изучает наука геометрия... 3. План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратны...