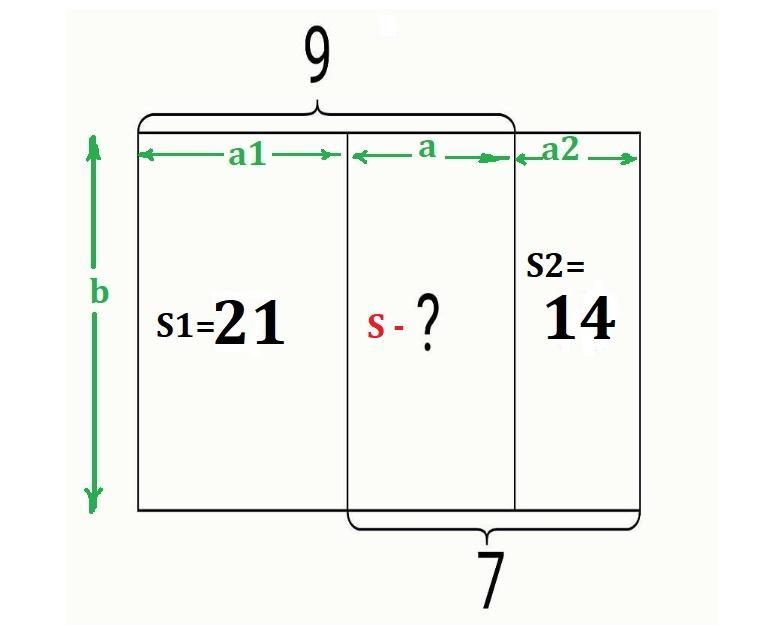
Прямоугольную полоску длины 16 разрезали на две полоски длин 9 и 7. Эти две полоски положили на стол так, как показано на рисунке. Известно, что площадь части стола, покрытой только левой полоской, равна 21, а площадь части стола, покрытой только правой полоской, равна 14. Найдите площадь части стола, покрытой обеими Полосками. 9 21 ? 14 7​

Ответ:
Площадь части стола, покрытой обеими полосками равна 10,5 ед²
Объяснение:
Прямоугольную полоску длины 16 разрезали на две полоски длин 9 и 7. Эти две полоски положили на стол так, как показано на рисунке. Известно, что площадь части стола, покрытой только левой полоской, равна S₁ = 21, а площадь части стола, покрытой только правой полоской, равна S₂=14. Найдите площадь части стола, покрытой обеими (S) полосками.

Площадь искомого прямоугольника находится по формуле:

S=ab,

где а - ширина искомой части, а b - её высота.

Мы видим, что высота у всех полосок одинаковая: b

Пусть ширина левой полоски равна а₁, при этом а₁=9-а. Тогда находим площадь левой полоски:
S₁=a₁b=(9-a)b
Так как по условию S₁=21, то получаем:
(9-a)b=21, или

9b-ab=21 (1)

Пусть ширина правой полоски равна а₂, при этом а₂=7-а. Тогда находим площадь правой полоски:
S₂=a₂b=(7-a)b
Так как по условию S₂=14, то получаем:
(7-a)b=14, или

7b-ab=14 (2)

Составим и решим систему из двух уравнений (1) и (2) методом сложения:



2b=7
b=3,5

Высота равна 3,5 ед.

Тогда а₁ = S₁ : b = 21 : 3,5 = 6 ед
Следовательно:
а = 9-а₁ = 9-6 = 3 ед
А искомая площадь:
S = ab = 3·3,5 = 10,5 ед²

#SPJ3