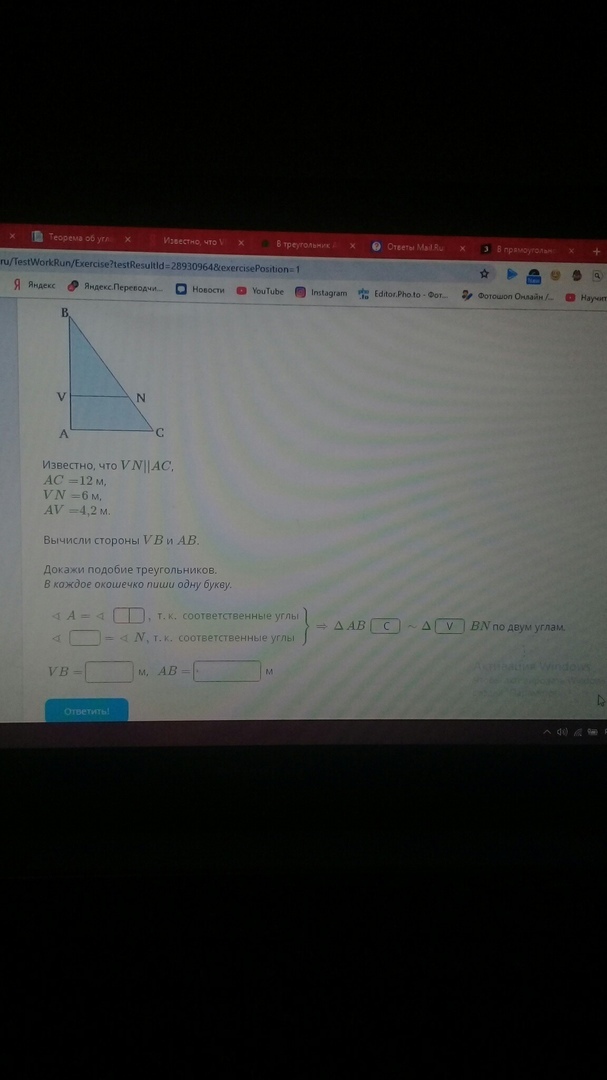
Дайте только ответ ...Известно, что VN||AC ,
AC= 12 м,
VN= 6 м,
AV= 4,2 м.
Вычисли стороны VB и AB .

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:

$VB = 4,2$ м; $AB = 8,4$ м.

Объяснение:

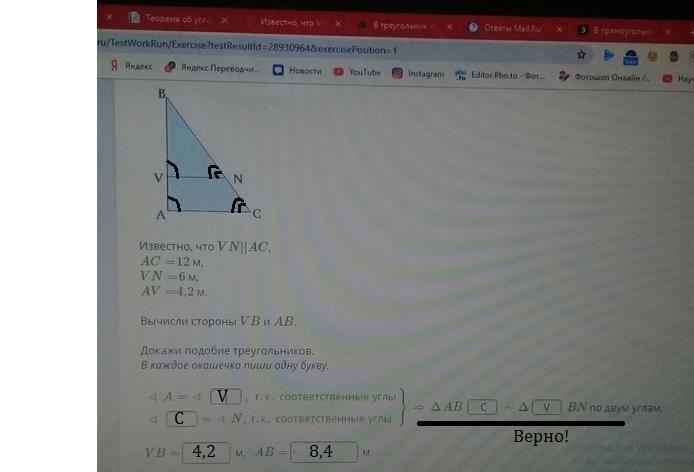
Рассмотрим 2 способа решения:
1 способ основан на подобии треугольников, как просят в условии.
2 способ основан на средней линии треугольника.
1 способ.
Решение, которое нужно предоставить картинке, которая дана в условии, на рисунке.
После того, как мы доказали подобие $\triangle ABC$ и $\triangle VBN$ , справедливо следующее равенство: $VN:AC = VB:AB$
Пусть $x$ м $- VB$ , тогда $(4,2 + x)$ м $- AB.$
$\dfrac = \dfrac\\\\ \dfrac = \dfrac \\\\ 5x + 21 = 10x\\\\-5x = -21\\\\x = 4,2$
$4,2$ м - VB.
Тогда $AB = VB + AV = 4,2 + 4,2 = 8,4$ м.
2 способ.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Средняя линия соединяет середины двух сторон треугольника.
Смотрим: $VN || AC$ , по условию; $AC = 2VN$ или $VN = AC:2$ , так как $VN = 6$ м, а $AC = 12$ м, по условию.
⇒ $VN$ - средняя линия $\triangle ABC$ .
⇒ $VB = AV = 4,2$ м $\Rightarrow AB = VB + AV = 4,2 + 4,2 = 8,4$ м.
=======================================================
Внимание! На рисунке изображен только 1 способ решения.

Хороший ответ

8 декабря 2022 20:27

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В прямоугольной трапеции ABCD(угол A=90°) известно, что AB=4см, AD=15 см, BC=12см. Найдите величину |вектор AB- вектор AD+ вектор BC|.... Помогитее,прошу))))Прямая MN является секущей для прямых AB и CD (M принадлежит AB, N принадлжит CD) угол AMN = 75 градусов . При каком значении угла... Если один из углов ромба равен 90 градусов,то такой ромб-квадрат.верно ли это утверждение?... Как сравнивать отрезки и углы?... Доказательство (!!!) теоремы о площади равностороннего треугольника....

Дайте только ответ ...Известно, что VN||AC , AC= 12 м, VN= 6 м, AV= 4,2 м. Вычисли стороны VB и AB .

Ответ:

Объяснение:

Дайте только ответ ...Известно, что VN||AC ,
AC= 12 м,
VN= 6 м,
AV= 4,2 м.
Вычисли стороны VB и AB .