Одна из сторон параллелограмма равна 12 другая равна 5, а тангенс одного из углов равен √2/4. Найти площадь

1 ответ

Посмотреть ответы

DevAdmin

1720

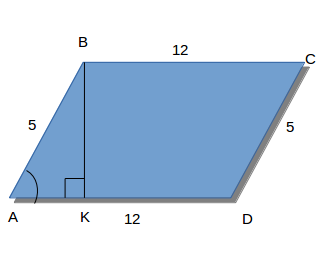
Дано: ABCD - паралелограмм; AB = 5(см); AD = 12(см) tgA = √2/2.

Найти S

Решение:

С вершины угла В проведём высоту ВК и получаем прямоугольный треугольник AKB

tg A - это отношение противолежащего катета к прилежащему, тоесть:

tg A = BK/ AK = √2/4

BK = √2 (см)

AK = 4 (см)

По т. Пифагора определяем гипотенузу

AB = √ (AK²+BK²) = √(4²+(√2)²)=√18

sin A = BK/AB = √2/√18 = 1/3

Отсюда площадь

S = AB * AD * sin A = 12*5*1/3 = 20 (см²).

Ответ: 20 (см²).

Хороший ответ

8 декабря 2022 21:09

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найдите координаты точки принадлежащей оси ординат и равноудалена от точек С (3, 2) и D(1; -6)... ДАЮ 40 БАЛЛОВ На тетрадном листочке в клеточку изображены четыре точки: A, B, C и D. Найди площадь треугольника ACD, если сторона клетки равна 6см.... Между сторонами угла АОВ, равного 140°, проведены лучи ОС и ом так, что угол АОС на 16° меньше угла ВОС, а OM — биссектриса угла Вос. Найдите величину... и последняя задача на сегодня :площадь сечения куба плоскостью,проходящей через концы трех ребер ,выходящих из одной вершины,равна 18*корень 3.Просят... Касательная к окружности,свойства касательной . доказательство любого свойства...