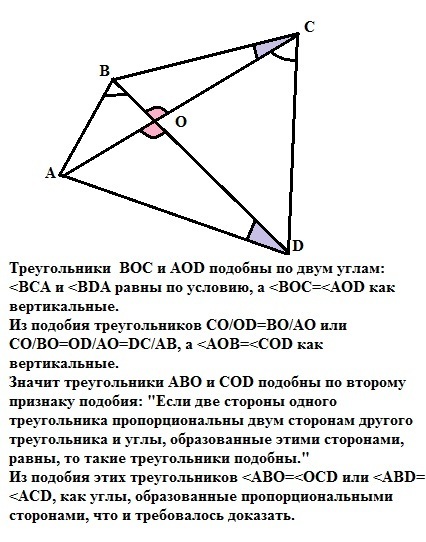
В выпуклом четырёхугольнике ABCD углы BCA и BDA равны. Докажите, что углы ABD и ACD так же равны.

Треугольники ВОС и АОD подобны по двум углам:
<BCA и <BDA равны по условию, а <BOC=<AOD как вертикальные.
Из подобия треугольников СО/OD=BO/AO или СО/ВО=OD/AO=DC/AB, а
<AOB=<COD как вертикальные.
Значит треугольники АВО и СOD подобны по второму признаку
подобия: "Если две стороны одного треугольника пропорциональны
двум сторонам другого треугольника и углы, образованные этими
сторонами, равны, то такие треугольники подобны."
Из подобия этих треугольников <ABO=<OCD или <ABD=<ACD,
как углы, образованные пропорциональными сторонами, что и требовалось доказать.