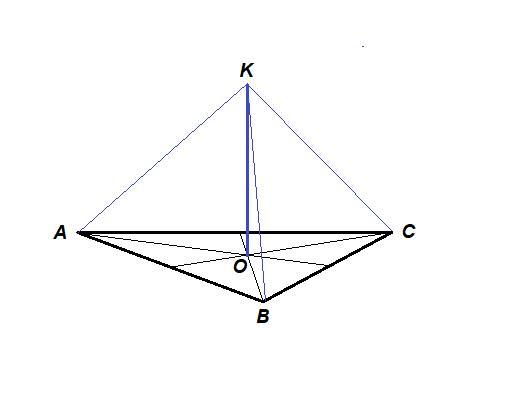
Точка K находится на расстоянии 4 см от каждой вершины правильного треугольника ABC. Найдите сторону треугольника, если точка K удалена от плоскости ABC на 2 см​

Ответ:
6 см
Пошаговое объяснение:
Пусть КО - перпендикуляр к плоскости АВС.
КО = 2 см.
ΔКОА = ΔКОВ = ΔКОС по катету и гипотенузе (КО - общий катет, КА = КВ = КС = 4 см по условию), значит точка О равноудалена от вершин треугольника АВС, т.е. О - центр описанной окружности.
Из прямоугольного треугольника АОК по теореме Пифагора:
АО = √(КА² - КО²) = √(4² - 2²) = √(16 - 4) = √12 = 2√3 см
Радиус окружности, описанной около правильного треугольника со стороной а:


а = 6 см