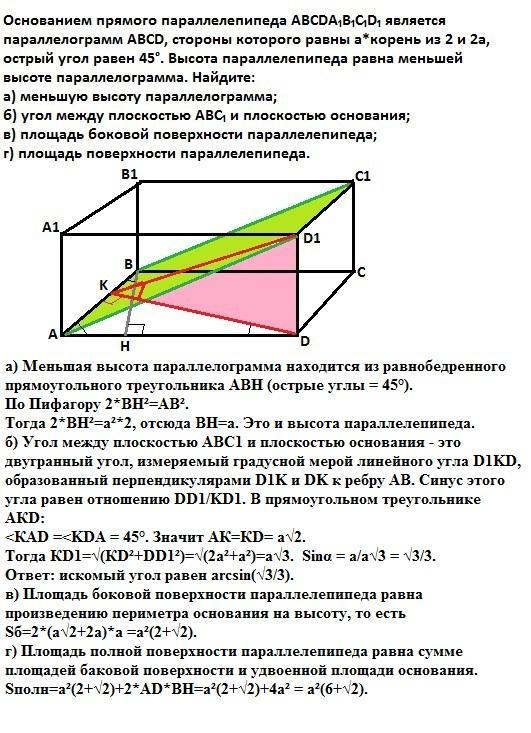
Основанием прямого параллелепипеда ABCDA₁B₁C₁D₁ являетсяпараллелограмм ABCD, стороны которого равны а*корень из 2 и 2а, острый
угол равен 45°. Высота параллелепипеда равна меньшей высоте
параллелограмма. Найдите:
а) меньшую высоту параллелограмма;
б) угол между плоскостью АВС₁ и плоскостью основания;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.

а) Меньшая высота параллелограмма находится из равнобедренного прямоугольного треугольника АВН (острые углы = 45°). По Пифагору 2*ВН²=АВ². Тогда 2*ВН²=а²*2, отсюда ВН=а. Это и высота параллелепипеда.
б) Угол между плоскостью АВС₁ и плоскостью основания - это двугранный угол, измеряемый градусной мерой линейного угла D1KD, образованный перпендикулярами D1K и DK к ребру АВ. Cинус этого угла равен отношению DD1/KD1. В прямоугольном треугольнике АКD:
<КАD =<KDA = 45°. Значит АК=КD= а√2.
Тогда КD1=√(КD²+DD1²)=√(2а²+а²)=а√3.
Sinα = a/а√3 = √3/3.
Ответ: искомый угол равен arcsin(√3/3).
в) Площадь боковой поверхности параллелепипеда равна произведению периметра основания на высоту, то есть Sб=2*(а√3+2а)*а =а²(2+√2).
г) Площадь полной поверхности параллелепипеда равна сумме площадей баковой поверхности и удвоенной площади основания. То есть
Sполн=а²(2+√2)+2*AD*BH=а²(2+√2)+4а² = а²(6+√2).