Лучшие помощники

Megamozg 2205 б
Matalya1 1800 б
DevAdmin 1720 б
arkasha_bortnikov 900 б
Dwayne_Johnson 870 б

Показать еще

·

Геометрия

10 декабря 2022 19:37

1264

Две окружности касаются внешним образом в точке A. Общая внешняя касательнаякасается этих окружностей в точках B и C. Докажите, что треугольник ABC прямоугольный.

P.S. Если можно с рисунком.

1 ответ

Посмотреть ответы

Радиус, проведенный в точку касания, перпендикулярен касательной
центры касающихся окружностей и их общая точка касания находятся на одной прямой)))

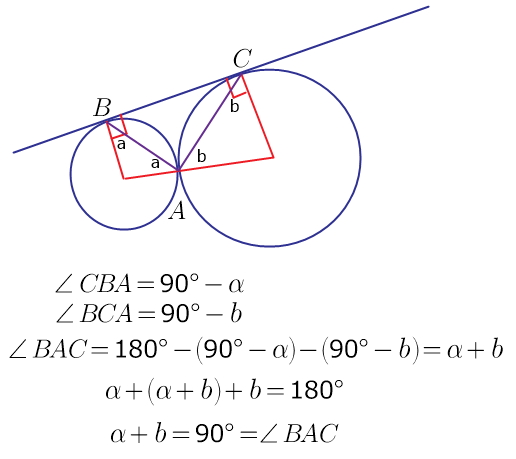
0

·

Хороший ответ

12 декабря 2022 19:37

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1.Найдите угол DAB. Ответ дайте в градусах... в прямоугольной трапеции меньшая боковая сторона равна 12см, а большая составляет с большим основанием угол 45 градусов. Найдите основание трапеции, е... Через вершину квадрата ABCD проведена прямая ВМ, перпендикулярная его плоскости. Докажите, что: 1) прямая AD перпендикулярна плоскости прямых АВ и ВМ;... №1. Средние линии треугольника относятся как 2:2:4, а периметр треугольника равен 45 см . Найдите стороны треугольника. №2.В прямоугольном треугольник... Нужно доказать что треугольники равны, по 2 признаку равенства треугольников...