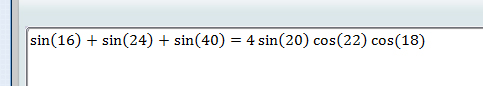Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
Ответ:
Пошаговое объяснение:

Преобразуем левую часть равенства, для этого воспользуемся следующей формулой


Воспользуемся формулой синуса двойного угла

и получим

воспользуемся следующей формулой


К сожалению получается другое тождество

Пошаговое объяснение:
Преобразуем левую часть равенства, для этого воспользуемся следующей формулой
Воспользуемся формулой синуса двойного угла
и получим
воспользуемся следующей формулой
К сожалению получается другое тождество
0
·
Хороший ответ
12 декабря 2022 20:50
Остались вопросы?
Еще вопросы по категории Математика
Сколько будет 23:3?...
Аня и Боря красят забор за 8 часов. Аня и Ваня красят этот же забор за 18 часов, а Боря и Ваня — за 24 часа. За сколько часов ребята покрасят забор, р...
1 8 мм это сколько см?...
Как сформулировать задание на основе '1 целой'?...
Составить 3 задачи на проценты по математике 6 класс с решением пожалуста и желательно объяснить...