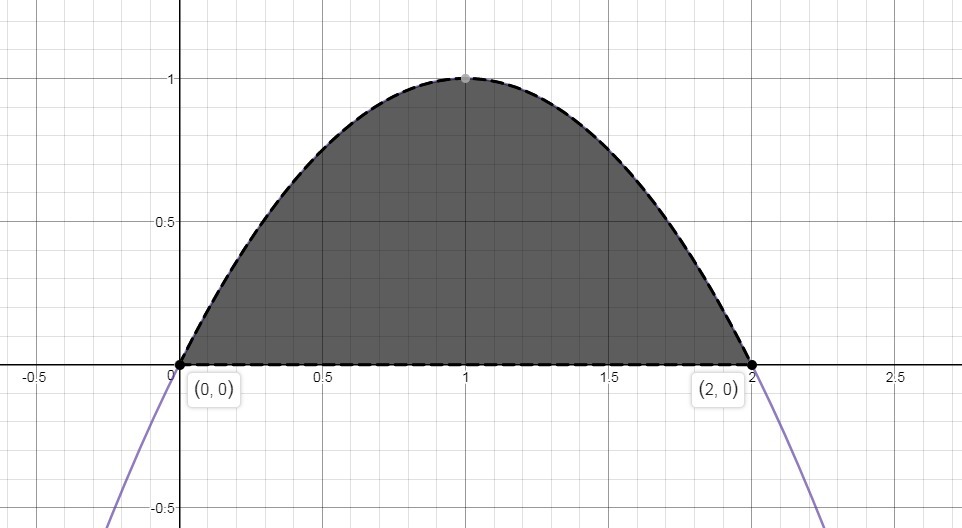
Вычислить площадь фигуры,ограниченной линиями y=2x-x^2 и y=0

1 ответ

Посмотреть ответы

DevAdmin

1720

Площадь фигуры ограниченной линиями равна определенному интегралу взятый в определенных пределах интегрирования.

Найдем пределы интегрирования
$2x-x^2 = 0 \\ \\ x(2-x) = 0 \\ \\ x_1 = 0 \ ; \ x_2 =2$

Теперь найдем площадь
$S = \int\limits^2_0 {(2x-x^2)} \, dx = (x^2- \fracx^3) |_0^2 = \\ \\ = 2^2- \frac*2^3 = 4- \frac = \frac$

Ответ:
$\frac$ кв. ед.

Хороший ответ

16 декабря 2022 15:03

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Сумма вертикальных углов AOB и COD, образованных при пересечении прямых AD и BC, равна 108°. Найдите угол BOD.... Найдите величину угла АОС, изображенного на рисунке, если ∠АВС=58°. Ответ дайте в градусах.... Дано: KABCDEM - правильная шестиугольная пирамида. КО - высота пирамиды. KT⊥AM; ∠KTO=60°. Найти отношение площадей ΔМКD и ΔMKC.... Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота — 6.... Даю 34 балла! Ответы с рисунками и полными объяснениями 1. Отрезок, длина которого равна 32 см, разделили на 3 неравных отрезка. Расстояние между сере...