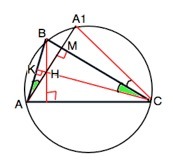
Точка Н - ортоцентр труегольника Авс.Прямая АН пересекает описанную около АВС окружность в точке А1. Докажите,что прямая ВС делит отрезок НА1 пополам.

1 ответ

Посмотреть ответы

DevAdmin

1720

Ортоцентр треугольника — точка пересечения его высот или их продолжений.
Обозначим высоту из С - СК, высоту из А - АМ.
∆АВМ~∆КВС - прямоугольные с общим острым углом при В.
Отсюда ∠ВАМ=∠ВСК.
Вписанные ∠А1СВ и ∠ВАА1 опираются на одну дугу ВА1 - след. они равны.
В ∆ НСА1 угол НМС прямой, отрезок СМ - высота и биссектриса - что является свойством высоты равнобедренного треугольника. Поэтому СМ еще и медиана, и НМ=МА1.
Прямая ВС делит НА1 пополам, ч.т.д.

Хороший ответ

16 декабря 2022 17:56

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Как можно найти радиус окружности, описанной около треугольника, если известны сторона треугольника 3см и противоположный ей угол: 1)120° 2)30° 3)135°... Диагональ боковой грани правильной треугольной призмы равна d и образует с диагональю боковой грани, которая выходит из той же вершины, угол β. Найдит... На клетчатой бумаге изображён треугольник. Найдите его площадь, если известно, что AB=5... В треугольнике ABC проведена средняя линия MN. Периметр треугольника CMN=8 см. Определи периметр треугольника ABC.... В треугольнике ABC угол С прямой, BC=3, cosB=0,6. Найдите АВ...