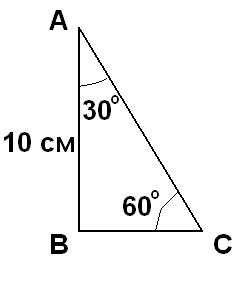
В прямоугольном треугольнике один из катетов равен 10, а угол лежащий напротив него равен 60 градусам. Найдите площадь треугольника.

1 ответ

Посмотреть ответы

DevAdmin

1705

Так как треугольник прямоугольный, то <A (см.рисунок во вложении) = 90 - <C = 90 – 60 = 30 градусов. Как известно, в прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы. Таким образом если этот катет, т.е. катет ВС обозначить Х, то гипотенуза т.е. сторона АС =2Х. По теореме Пифагора (АС)^2 = (AB)^2 + (BC)^2. Подставив в это уравнение принятые и известный отрезки имеем (2Х)² = 10² + X², или 4Х²= 10²+ X² или 3Х²= 100. Отсюда Х²= 100/3 и малый катет, т.е. Х = √(100\3) = 10/√3. Площадь прямоугольного треугольника равна половине произведения его катетов. Т.е. S = (АВ*ВС)/2 = 10*10/2√3 = 50/√3

Хороший ответ

16 декабря 2022 19:02

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Про невырожденный треугольник ABC известно, что AB=3.5, AC=2.4, а длина стороны BC выражается целым числом n. Чему может быть равно n? Если ответов не... Основания трапеции равны 4 и 9. найдите отрезок,соединяющий середины диагоналей трапеции... Подскажите, пожалуйста, геометрия, 10 класс.... В равнобедренной трапеции один из углов равен 60градусов, боковая сторона равна 8см,а меньшее оснавание 7см.найдите среднюю линию трапеции.... Помогите пожалуйста, нужно доказать подобность треугольников...