Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
14 декабря 2022 23:09
893
Найти три последние цифры числа 7 в степени 9999
1
ответ
1 способ. Если разрешается пользоваться теоремой Эйлера, то все несложно. Решение прицеплено в картинке.
2 способ (более скучный, зато совсем школьный).
Будем вычислять три последние цифры у различных степеней семерки до тех пор, пока эти три цифры не станут 001.
В первой колонке степень n, а во второй - три последних цифры числа 7ⁿ:
1 7
2 49
3 343
4 401
5 807
6 649
7 543
8 801
9 607
10 249
11 743
12 201
13 407
14 849
15 943
16 601
17 207
18 449
19 143
20 001
Т.е. мы видим, что число 7²⁰ заканчивается на ...001, а значит и его любая степень тоже заканчивается на ...001. Итак, 7⁹⁹⁹⁹=(7²⁰)⁴⁹⁹·7¹⁹, т.е. последние 3 цифры числа 7⁹⁹⁹⁹ будут такими же, как у числа 7¹⁹, т.е. 143.
Надо заметить, что это не совсем "честный" способ. Если заранее не знать, что уже на 20-ой степени мы получим 001, то вполне могло оказаться, что 001 не появится через относительно небольшое количество шагов. Поэтому, когда надо узнать несколько последних цифр числа без компьютера или подсказок, с этим методом рискованно связываться.
2 способ (более скучный, зато совсем школьный).
Будем вычислять три последние цифры у различных степеней семерки до тех пор, пока эти три цифры не станут 001.
В первой колонке степень n, а во второй - три последних цифры числа 7ⁿ:
1 7
2 49
3 343
4 401
5 807
6 649
7 543
8 801
9 607
10 249
11 743
12 201
13 407
14 849
15 943
16 601
17 207
18 449
19 143
20 001
Т.е. мы видим, что число 7²⁰ заканчивается на ...001, а значит и его любая степень тоже заканчивается на ...001. Итак, 7⁹⁹⁹⁹=(7²⁰)⁴⁹⁹·7¹⁹, т.е. последние 3 цифры числа 7⁹⁹⁹⁹ будут такими же, как у числа 7¹⁹, т.е. 143.
Надо заметить, что это не совсем "честный" способ. Если заранее не знать, что уже на 20-ой степени мы получим 001, то вполне могло оказаться, что 001 не появится через относительно небольшое количество шагов. Поэтому, когда надо узнать несколько последних цифр числа без компьютера или подсказок, с этим методом рискованно связываться.
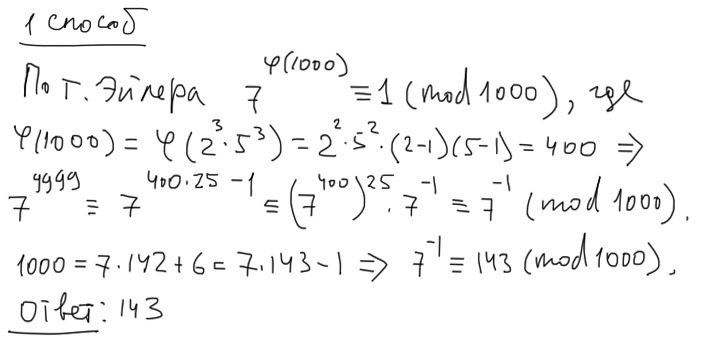
0
·
Хороший ответ
16 декабря 2022 23:09
Остались вопросы?