Найдите высоту треугольника ABC, опущенную насторону АС, если стороны квадратных клеток равны
√10

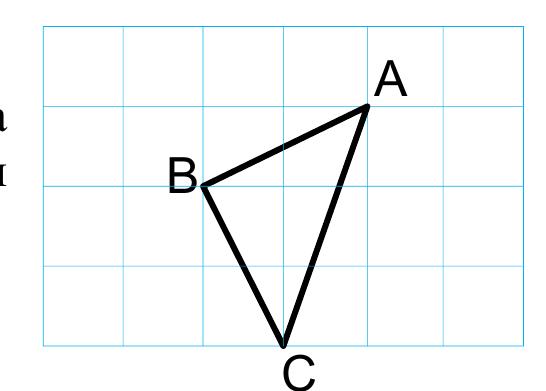
1 ответ

Посмотреть ответы

Megamozg

2205

В ΔАВС
АВ² = (√10)²+(2√10)²=50 ⇒ АВ=√50
ВС² = (√10)²+(2√10)²=50 ⇒ АВ=√50
АС² = ( (√10)²+(3√10)²=100 ⇒ АС=10

Высота проведенная к основанию АС делит ΔАВС на два равных прямоугольных треугольника с гипотенузой √50 и катетом 10:2=5
h² = (√50)² - (√25)²=25
h=5

Хороший ответ

17 декабря 2022 19:02

Остались вопросы?

Найти нужный

Еще вопросы по категории Алгебра

решите производную с максимальным объяснением пожалуйста... Найти сумму бесконечной геометрической прогрессии 28; -14, 7, ....... Помогите,пожалуйста.. 1.Найти дельта y, если х нулевое=1, а дельта х=0,1 при y=x^2-1; 2.Тело движется прямолинейно по закону S(t)=1+2t^2.Вычислите ско... Решить уравнения: 7-x/2=3+7x/2 x/2 это дробь,7x/2 это дробь... Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 138. РЕШИТЕ ПОЖАЛУЙСТА)))...

Найдите высоту треугольника ABC, опущенную насторону АС, если стороны квадратных клеток равны √10

Найдите высоту треугольника ABC, опущенную насторону АС, если стороны квадратных клеток равны
√10