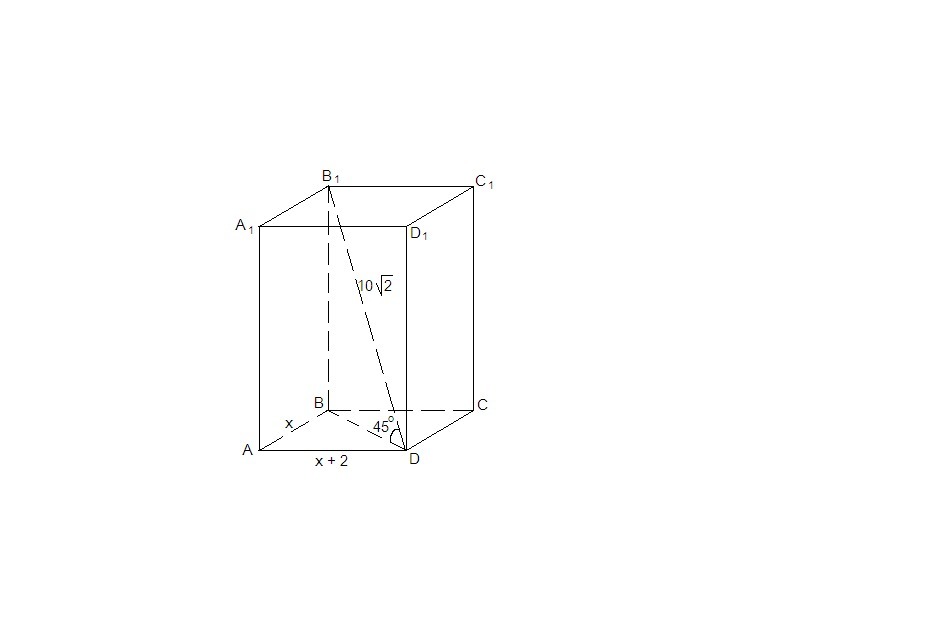
Диагональ прямоугольного параллелепипеда равна 10 корней из двух (см) и образует с плоскостью основания 45 градусов.Найти объем параллелепипеда,если одна сторона основания на 2см больше другой.

1 ответ

Посмотреть ответы

DevAdmin

1690

Все грани прямоугольного параллелепипеда - прямоугольники. ВВ₁⊥(АВС)⇒
BD - проекция диагонали В₁D на плоскость основания. Тогда ∠В₁DB = 45°.
ΔВ₁DB прямоугольный и, значит, равнобедренный.
BD = BВ₁ = В₁D/√2 = 10 cм

ΔABD:
∠BAD = 90°. Пусть АВ = х, тогда AD = х + 2. По теореме Пифагора
BD² = AB² + AD²
100 = x² + (x + 2)²
2x² + 4x - 96 = 0
x² + 2x - 48 = 0
x = 6 или х = - 8 по теореме Виета
По смыслу задачи подходит х = 6
АВ = 6 см, AD = 8 см.
V = AB · AD · AA₁ = 6 · 8 · 10 = 480 cм³

Хороший ответ

18 декабря 2022 00:05

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой 2 корень 3... На рисунке изображён график функции у=-х2+4. Какие из данных прямых не имеют с графиком этой функции ни одной общей точки? Укажите их номера. 1) у=х 2... Высота BM проведенная из вершины угла ромба ABCD образует со стороной AB угол = 30 градусов.длина диагонали AC равна 6 см. Найдите AM , если точка М л... В трапеции ABCD известно,что AD=8,BC=7,а её площадь равна 45.Найдите площадь треугольника ABC... По данным рисунка 119 найдите угол 1. Помогите завтра надо!...