Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
16 декабря 2022 02:59
1038
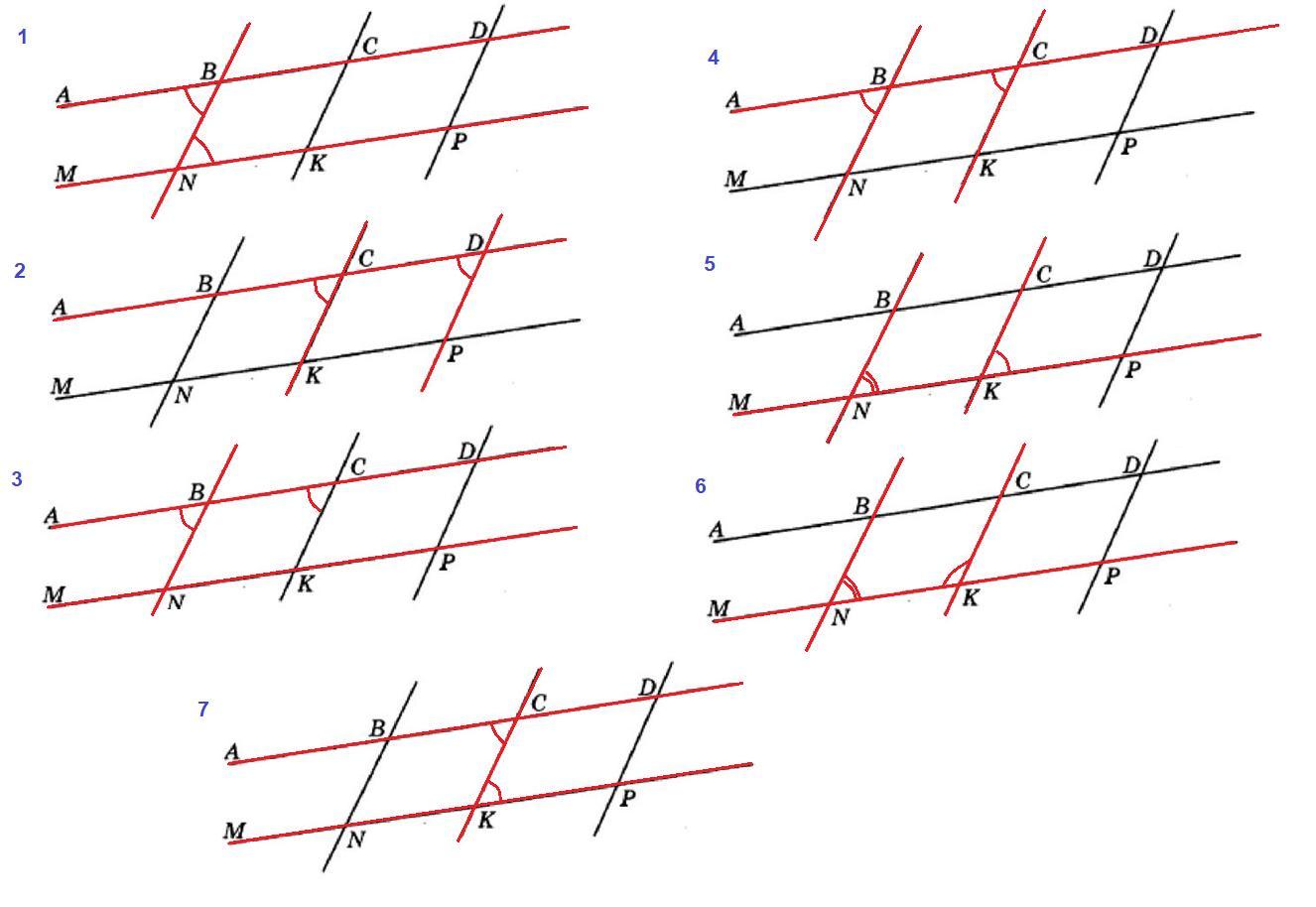
Используя рисунок, запишите номера верных утверждений:1) ABN и BNK –накрест лежащие при прямых АВ и MN и секущей BN.
2) ВСК и CDP – соответственные при прямых СК и DP и секущей CD.
3) ABN и BCK – односторонние при прямых АВ и MN и секущей ВN.
4) Если ABN = BCK, то BN || СК.
5) Если BNK + CKP = 180°, то BN || CK.
6) Если BNK + NKC = 180°, то BN || СК.
7) Если BCK = CKP, то ВС || NK.

1
ответ
Ответ:
1, 2, 4, 6, 7.
Объяснение:
Признаки параллельности прямых:
1) ∠ABN и ∠BNK – накрест лежащие при прямых АВ и MN и секущей BN.
Верно.
2) ∠ВСК и ∠CDP – соответственные при прямых СК и DP и секущей CD.
Верно.
3) ∠ABN и ∠BCK – односторонние при прямых АВ и MN и секущей ВN.
Неверно. Это соответственные углы при прямых BN и СК и секущей ВС.
4) Если ∠ABN = ∠BCK, то BN || СК.
Верно, так как эти углы соответственные при прямых BN и СК и секущей ВС.
5) Если ∠BNK + ∠CKP = 180°, то BN || CK.
Неверно. Эти углы соответственные при прямых BN и СК и секущей NK. А прямые параллельны, если соответственные углы равны.
6) Если ∠BNK + ∠NKC = 180°, то BN || СК.
Верно, так как эти углы - внутренние односторонние при прямых BN и СК и секущей NK.
7) Если ∠BCK = ∠CKP, то ВС || NK.
Верно, так как эти углы внутренние накрест лежащие при прямых ВС и NK и секущей СК.
1, 2, 4, 6, 7.
Объяснение:
Признаки параллельности прямых:
- Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
- Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
- Если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
1) ∠ABN и ∠BNK – накрест лежащие при прямых АВ и MN и секущей BN.
Верно.
2) ∠ВСК и ∠CDP – соответственные при прямых СК и DP и секущей CD.
Верно.
3) ∠ABN и ∠BCK – односторонние при прямых АВ и MN и секущей ВN.
Неверно. Это соответственные углы при прямых BN и СК и секущей ВС.
4) Если ∠ABN = ∠BCK, то BN || СК.
Верно, так как эти углы соответственные при прямых BN и СК и секущей ВС.
5) Если ∠BNK + ∠CKP = 180°, то BN || CK.
Неверно. Эти углы соответственные при прямых BN и СК и секущей NK. А прямые параллельны, если соответственные углы равны.
6) Если ∠BNK + ∠NKC = 180°, то BN || СК.
Верно, так как эти углы - внутренние односторонние при прямых BN и СК и секущей NK.
7) Если ∠BCK = ∠CKP, то ВС || NK.
Верно, так как эти углы внутренние накрест лежащие при прямых ВС и NK и секущей СК.
0
·
Хороший ответ
18 декабря 2022 02:59
Остались вопросы?
Еще вопросы по категории Геометрия
найдите длину хорды окружности радиусом 13 см если расстояние от центра окружности до хорды равно 5 см.Пожалуйста,помогите)...
Что означает знак э в геометрии?...
Решите задачу. Запишите подробное решение и ответ. В прямоугольном треугольнике ABC катет AC = 20 см, катет CB = 15 см. Найдите, во сколько раз длина...
расстояние между двумя параллельными плоскостями равно 4дм. точки A и B лежат в данных плоскостях, а угол между отрезком AB и его проекцией на одну из...
Четырехугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах....