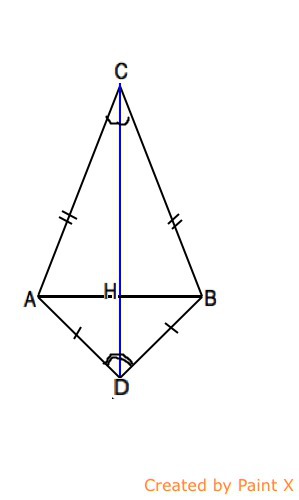
равнобедренные треугольники ABC и ABD имеют общее основание AB.Докажите что отрезок CD проходит через середину AB. Пожалуйста напишите подробное доказательство.

Сделаем рисунок и соединим вершины С и D данных треугольников. Обозначим точку пересечения CD с АВ буквой Н.
Рассмотрим ∆ CAD и ∆ CBD
АС=СВ и AD=BD по условию; сторона СD- общая.
∆ CAD = ∆ CBD по 3-му признаку равенства треугольников.
Тогда ∠АСD=∠BCD;
∠CDA=∠CDB.
СD- биссектриса углов при вершинах С и D равнобедренных треугольников.
По свойству равнобедренных треугольников биссектриса, проведенная к основанию, является еще и высотой и медианой. ⇒
СН и DН - медианы этих треугольников, а поскольку у них общее основание АВ, то CD проходит через середину АВ, ч.т.д.