Докажите теорему:если в треугольнике биссектриса является медианой,то треугольник равнобедренный.

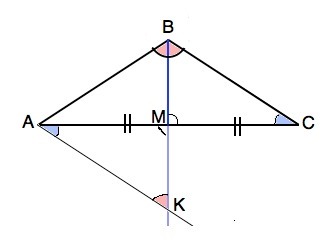
Обозначим треугольник АВС; ВМ -биссектриса и медиана.
Проведем из А параллельно ВС прямую до пересечения с прямой ВМ в точке К.
Рассмотрим треугольники АМК и ВМС. АМ=СМ (т.к. ВМ – медиана), углы этих треугольников при М равны как вертикальные, ∠ВСМ=∠КАМ как накрестлежащие при пересечении параллельных (по построению) прямых ВС и АК секущей АС.
Следовательно, ∆ АКМ=∆ ВСМ по второму признаку равенства треугольников. ⇒
АК=ВС.
Т.к. ВМ биссектриса угла АВС, ∠АВМ=∠СВМ, а из равенства треугольников АКМ и СВМ углы при основании ВК треугольника ВАК равны – ∆ ВАК равнобедренный и АВ=АК.
Из доказанного выше АК=ВС, следовательно, АВ=ВС.⇒
∆ АВС равнобедренный, что и требовалось доказать.