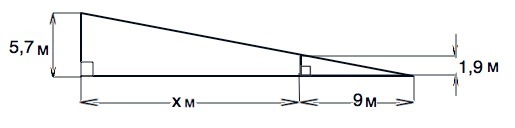
На каком расстоянии от фонаря расположенного на высоте 5 7 м стоит человек ростом 1.9 м если длина его тени равна 9м

1 ответ

Посмотреть ответы

Megamozg

2205

Задача на подобие треугольников.
Столб и человек по отношению к земле - перпендикулярны.
Если от вершины столба через голову человека провести прямую к концу его тени, получим подобные ( по общему острому углу) треугольники.
Высоту человека и столба примем за катеты прямоугольных треугольников, тень человека и расстояние от основания столба до конца тени человека - вторые катеты.
Длина тени столба равна сумме расстояния от его основания до человека и тени человека ( см. рисунок).
Сходственные стороны подобных треугольников пропорциональны. Составим пропорцию:
5,7:1,9=(х+9):9
5,7•9=1,9х+1,9•9
1,9х=9•(5,7-1,9)
1,9х=9•3,8
х=18 м- на таком расстоянии от столба стоит человек.

Хороший ответ

28 декабря 2022 04:35

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Даны стороны треугольников PQR и ABC: PQ= 16 см, QR=20 см, PR=28 см и АВ =12 см , ВС=15 см , АС=21 см .Найдите отношение площадей этих треугольников .... Помогите пожалуйста! Площадь правильного шестиугольника АBCDEF равна 144.Нужно найти площадь треугольника АВС (8бал).... В трапеции ABCD AB=CD, ∠BDA=67∘ и ∠BDC=28∘. Найдите угол ABD. Ответ дайте в градусах.... Найдите площадь прямоугольного треугольника ,если его катеты равны 3см и 5см... Верно ли утверждение, что прямая, лежащая в одной из параллельных плоскостей, параллельна другой плоскости?(обоснуйте ответ)...