Медиана прямоугольного треугольника, проведённая к гипотенузе , разбивает его на треугольника с периметрами 8 и 9. Найти стороны треугольника.

1 ответ

Посмотреть ответы

Megamozg

2205

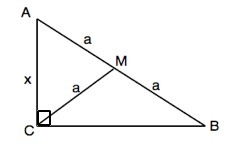
Обозначим треугольник АВС, угол С=90°; медиана СМ
Примем СМ=а.
Медиана прямоугольного треугольника равна половине гипотенузы.
Поэтому АМ=ВМ=СМ=а ⇒
Гипотенуза АВ=2а
Примем катет АС=х, тогда периметр ∆ АМС=АМ+СМ+АС=2а+х
2а+х=8
Р(СМВ)=2а+СВ
Р(СМВ)- Р(СМА)=9-8=1, следовательно, СВ=АС+1=х+1
Из ∆ АМС=2а=8-х
Так как АВ=2а, то АВ=8-х
По т.Пифагора АВ²=АС²+ВС²
(8-х)²=х²+(х+1)²
64-16х+х*=х²+х²+2х+1 --
х²+18х-63=0
Решив квадратное уравнение, получим х1=3, х2=-21( не подходит)⇒
АС=3,
ВС=3+1=4.
Гипотенуза АВ=8-3=5

Хороший ответ

28 декабря 2022 06:42

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

На продолжении стороны АВ равнобедренного треугольника АВС с основанием АС отметили точку D так, что AD = АС и точка А находится между точками В и D.... Сторона равностороннего треугольника равна 16√3. Найдите его медиану.... в прямоугольном треугольнике гипотенуза равна 70,а один из острых углов равен 45.найдите площадь треугольника.... Обчислить: 1) 4 cos 90° + 2 cos 180° - tg 180°; 2) cos 0° - cos 180° + sin 90°.... Верно ли утверждение, что прямая, лежащая в одной из параллельных плоскостей, параллельна другой плоскости?(обоснуйте ответ)...