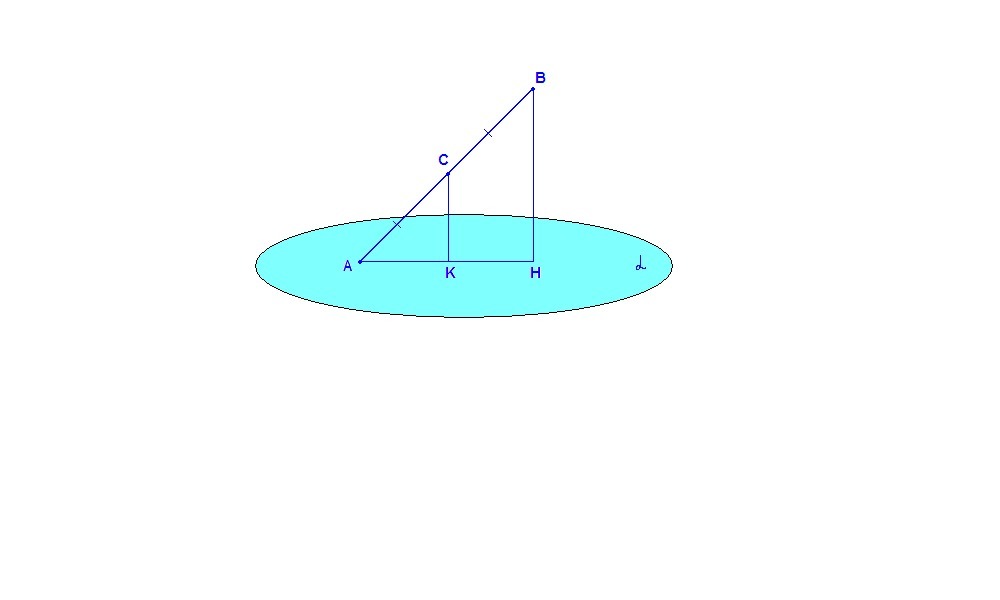
один конец данного отрезка лежит в плоскости α, а другой находится от нее на расстоянии 6 см. Найдите расстояние от середины данного отрезка до плоскости α.

Расстояние от точки до плоскости - длина перпендикуляра, проведенного из точки к плоскости.
Проведем ВН⊥α.
ВН = 6 см.
Пусть С - середина отрезка АВ.
СК⊥α.
Два перпендикуляра, проведенные к одной плоскости, параллельны, значит прямые ВН и СК задают плоскость, в которой лежат две точки отрезка АВ, значит и весь отрезок лежит в этой плоскости.
Итак, в ΔАВН: С - середина АВ и СК║ВН, значит СК - средняя линия ΔАВН по признаку.
СК = ВН/2 = 3 см