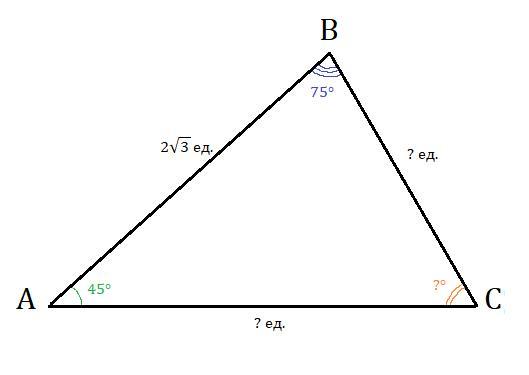
Решить треугольник ABC. Если угол А=45 градусов,Угол В=75 градусов,АВ=2 и корень из 3

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:

$\angle C = ^{\circ};$ $AC = \sqrt + \sqrt$ ; $BC = 2\sqrt$ .

Объяснение:

1) Найдём $\angle C$ :
Сумма внутренних углов треугольника равна $^{\circ}$ .
$\Rightarrow \angle C = ^{\circ} - (\angle A + \angle B) = ^{\circ} - (^{\circ} + ^{\circ}) = ^{\circ}$
2) Найдём $BC$ :
По теореме синусов: $\dfrac{\sin(C)} = \dfrac{\sin(A)}$
$\Rightarrow BC = \dfrac{\sin(C)} = \dfrac \cdot \sin(^{\circ})}{\sin(^{\circ})} = \dfrac\cdot \dfrac{\sqrt } }{\dfrac{\sqrt } }=\sqrt \cdot\sqrt\cdot \dfrac{\sqrt } = 2\sqrt$
3) Найдём $AC$ :
Пусть $x$ - $AC.$
По теореме косинусов:
$AB = \sqrt{^ + ^ - 2 \cdot BC \cdot AC \cdot \cos(C)}$
$(2\sqrt)^ = (2\sqrt)^ + x^ - 2 \cdot (2\sqrt) \cdot x \cdot cos(60^{\circ})$
$12 = 8 + x^ - (2\sqrt)x\\12 - 8 - x^ +( 2\sqrt) x = 0\\-x^ + (2\sqrt) x +4 = 0\\x^ - (2\sqrt) x - 4 = 0$
$\\x = \dfrac{-(-2\sqrt)\pm\sqrt{(-2\sqrt)^-4\cdot1\cdot(-4) } }$
$x = \dfrac\pm\sqrt } \\x = \dfrac \pm2\sqrt } \\ x_ = \sqrt + \sqrt \\x_ = \sqrt - \sqrt$
Так как $\sqrt > \sqrt \Rightarrow$ $\sqrt - \sqrt < 0$ (т.е. в результате этого действия получится отрицательное число) $\Rightarrow x_2$ не подходит.
$\Rightarrow$ $AC = \sqrt + \sqrt$ .

Хороший ответ

29 декабря 2022 00:51

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Помоогите срочно Биссектриса равностороннего треугольника равна половине стороны треугольника.Это утверждение... 1.может быть верно 2.верно всегда 3.н... 1. В прямоугольном треугольнике DАS угол S равен 30°, угол А равен 90°. Найдите гипотенузу DS этого треугольника, если катет DА равен 8,5см.... В Кубе ABCDA1B1C1D1 найдите угол между прямыми BA1 и AC. Ответ дайте в градусах.... ПОМОГИТЕ ПОЖАЛУЙСТА, 10-11 КЛАСС!!! Постройте сечение прямой призмы ABCA1B1C1 плоскостью, параллельной ребру основания BC, проходящей через вершину ос... Прямоугольный параллелипипед описан около сферы радиусом 17. Найдите его объем....