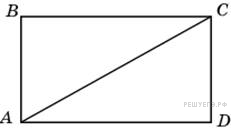
периметр прямоугольника равен 34, а площадь равна 60. Найти диагональ этого треугольника. ПРОШУ ПОДРОБНО!!!!

1 ответ

Посмотреть ответы

Megamozg

2205

Pabcd = 2(a + b) = 34
Sabcd = a·b = 60 система уравнений

a + b = 17
ab = 60

b = 17 - a
a(17 - a) = 60 решаем второе уравнение

a² - 17a + 60 = 0
D = 289 - 240 = 49
a = (17 - 7)/2 = 5 или a = (17 + 7)/2 = 12
b = 12 b = 5

Пусть АВ = 5 см, ВС = 12 см.
ΔАВС: ∠АВС = 90°, по теореме Пифагора
АС = √(АВ² + ВС²) = √(25 + 144) = √169 = 13 см

Хороший ответ

29 декабря 2022 02:56

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Постройте график с таблицей значений y=lgx СРОЧНО... Используя данные приведенные на рисунке укажите номера верных утверждений: 1) треугАВС- прямоугольный 2)треугАВС-равнобедренный 3 уг1-внешний угол т... список заданий викторины состоял из 33 вопросов. за каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 11 очков, а... сторона АВ треугольнька АВС равна 42 .противолежащей ей угол С равен 150. найдите радиус окружности,описаной около треугольника... Окружность с центром в точке О описана около равнобедренного треугольника АВС , в котором АВ=ВС и угол АВС=138 градусов. Найдите величину угла ВОС. От...