Диагональ правельной четырёхугольной призмы равна а и образует сплоскостью боковой грани угол 30 градусов. Найти:а) сторону основания
призмы. б) угол между диагональю призмы и плоскостью основания. в)
площадь боковой поверхности призмы. г) площадь сечения призмы с
плоскостью проходящей через диагональ основания параллельно диагонали
призмы.

1 ответ

Посмотреть ответы

Megamozg

2200

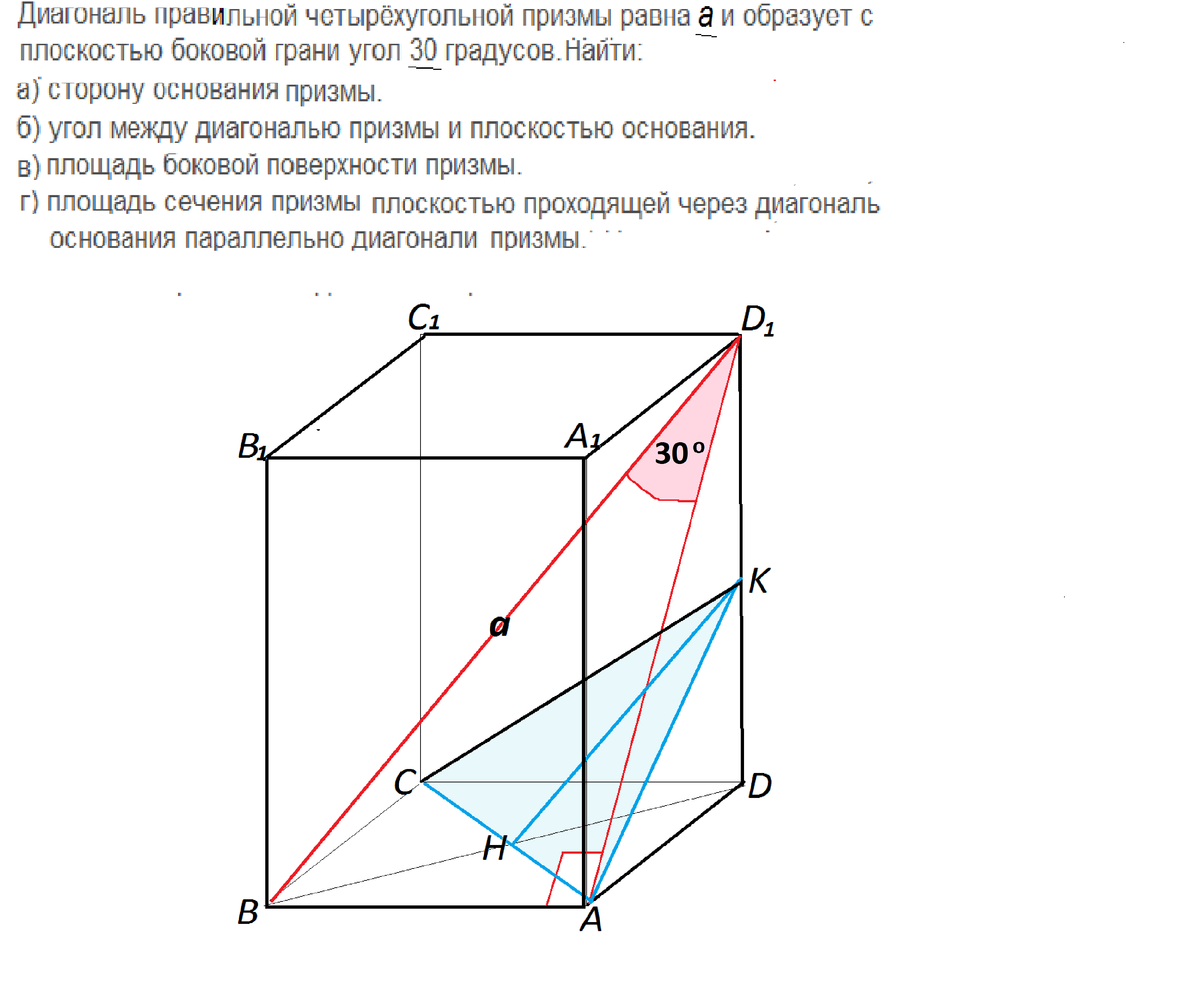
Диагональ правильной четырёхугольной призмы равна а и образует с
плоскостью боковой грани угол 30°. Найти:
а) сторону основания
призмы.
б) угол между диагональю призмы и плоскостью основания
в) площадь боковой поверхности призмы.
г) площадь сечения призмы плоскостью, проходящей через диагональ основания параллельно диагонали призмы.

В основаниях правильной призмы - правильные многоугольники, а боковые грани - прямоугольники. Следовательно, ее боковые ребра перпендикулярны основанию.
Треугольник ВD1А - прямоугольный (в основании призмы - квадрат, и ребра перпендикулярны основанию.
а) Сторона основания противолежит углу 30°, поэтому АВ=а*sin 30=a/2
б) угол между диагональю призмы и плоскостью основания - это угол между диагональю ВD1 призмы и диагональю ВD основания.
ВD как диагональ квадрата равна а√2):2
cos D1BD=BD:BD1=( а√2):2):a=(√2):2),
и это косинус 45 градусов.
в) площадь боковой поверхности призмы находят произведением высоты на периметр основания:
S бок=DD1*AB= (а√2):2)*4*a/2=a²√2
г) Сечение призмы, площадь которого надо найти, это треугольник АСК.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости. Верным является и обратное утверждение.
Высота КН - средняя линия прямоугольного треугольника BDD1. Она параллельна диагонали призмы, а само сечение проходит через диагональ АС основания.
S Δ(АСК)=КН*СА:2
SΔ (АСК)=(0,5а*а√2):2):2=(а²√2):8
--------
[email protected]

Хороший ответ

29 декабря 2022 03:34

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Дано: треугольник abc Ab=3, ac=4, cb= корень из 13 Bm-медиана. Найти: bm... В правильной треугольной пирамиде SABC N — середина ребра BC, S — вершина. Известно, что AB=1, а площадь боковой поверхности равна 3. Найдите длину от... MN и MK - отрезки касательных, проведённых к окружности радиусом 5 см. Найдите длины отрезков MN и MK, если MO = 13 см... Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани... Периметр ромба 68см, а одна из его диагоналей равна 30см. найдите длину другой диагонали ромба....