Докажите, что середины сторон произвольного четырёхугольника являются вершинами параллелограмма.

2 ответа

Посмотреть ответы

Megamozg

2205

Смотри вложение.
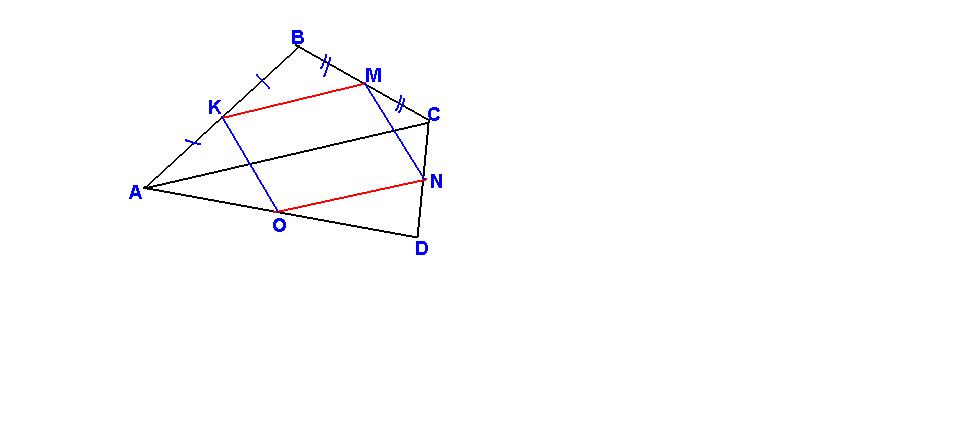
КМ средняя линия треуг. АВС(по определению), тогда КМ = АС/2 и КМ параллельна АС
ON средняя линия треуг. ADC, значит ON = AC/2 и ON параллельна АС
Получаем, что KM=ON и KM параллельна ON(это признак!)Если две стороны четырехуг. равны и параллельны, то четырехуг. - параллелограмм.
Значит KMNO параллелограм.

Хороший ответ

29 декабря 2022 06:13

Megamozg

2205

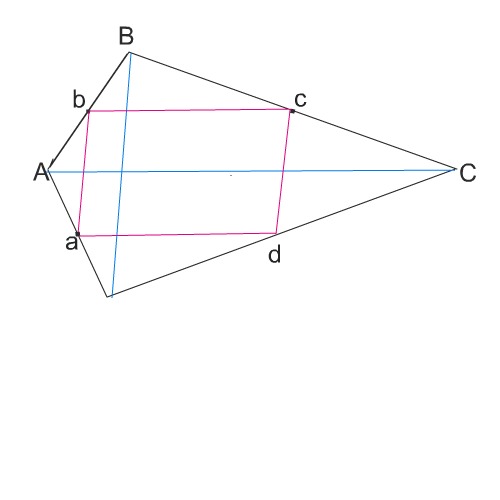
Проведем диагонали в этом четырехугольнике.
Получим четыре треугольника. (См. рисунок)
Если соединить середины четырехугольника, получим среднюю линию каждого из этих треугольников, причем эти средние линии попарно равны и параллельны, так как у пар треугольников с противоположными вершинами - общие основания.
Четырехугольник, стороны которого попарно параллельны - параллелограмм. Ч.т.д.

29 декабря 2022 06:13

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

СРОЧНО!!ПОЖАЛУЙСТА,ПОМОГИТЕ! даны две правильные четырехугольные пирамиды. объем первой пирамиды равен 9. у второй пирамиды высота в 1,5 раза больше ,... В Кубе ABCDA1B1C1D1 найдите угол между прямыми BA1 и AC. Ответ дайте в градусах.... Отрезок АК-биссектриса треугольника САЕ. Через точку К проведена прямая,параллельная стороне СА и пересекающая сторону АЕ в точке N. Найдите углы треу... Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота — 6.... Из точки D, которая лежит вне плоскости α, проведены к этой плоскости наклонные DK и DB, образующие с ней углы 45° и 60° соответственно. Найдите длину...