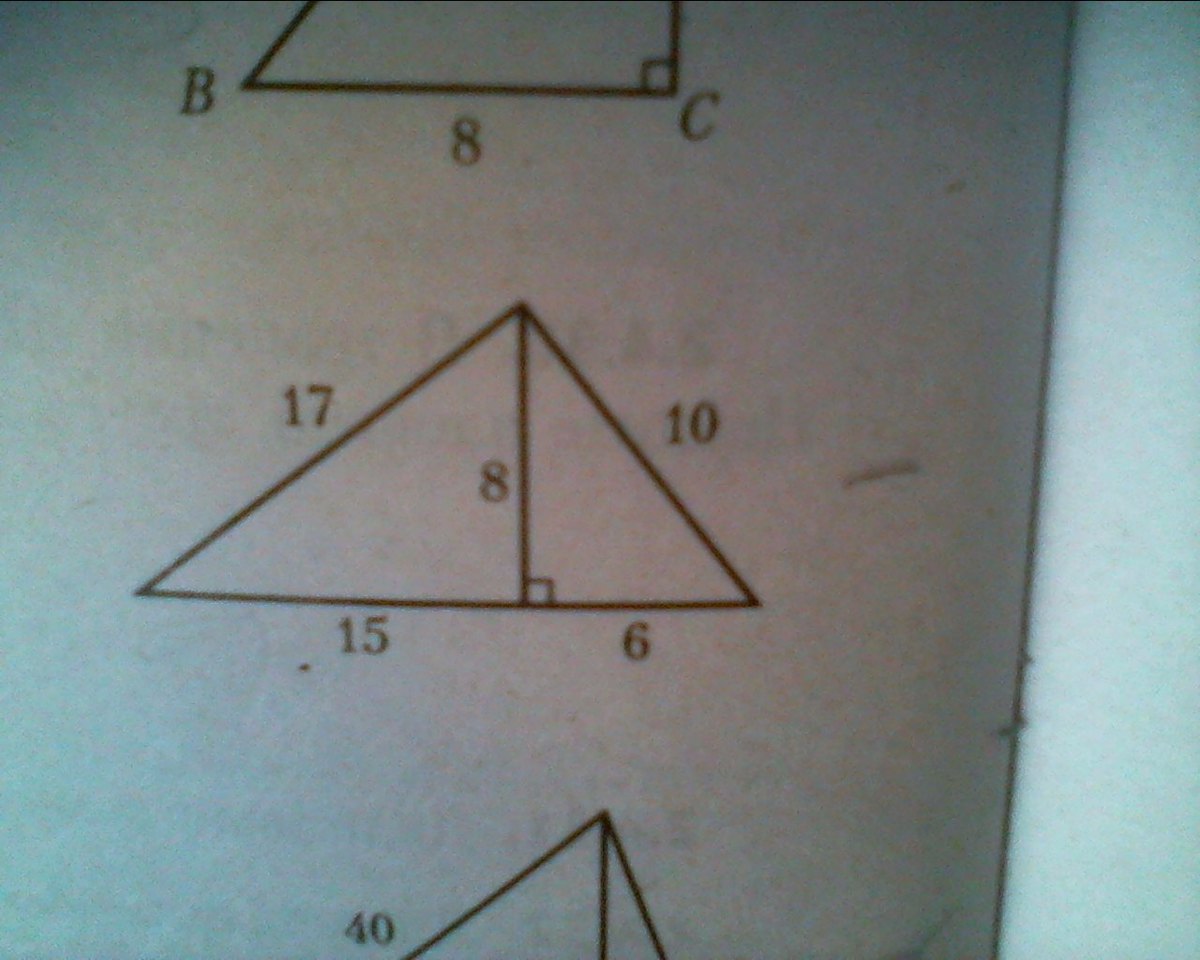
Найдите площадь треугольника изображенного на рисунке . ( объясните по подробнее пожалуйста )

2 ответа

Посмотреть ответы

Megamozg

2205

Площадь треугольника равна половине произведения основания на высоту.
основание равно 15+6=21
высота равна 8
S=1/2*21*8=21*4=84

Можно по другому
Большой треугольник состоит из 2 прямоугольных треугольников.
Площадь прямоугольного треугольника равна половине произведения катетов.
S1=1/2*15*8=60
S2=1/2*6*8=24
S=S1+S2=60+24=84

Хороший ответ

29 декабря 2022 07:20

DevAdmin

1720

Существует формула по определению площади треугольника, которую надо знать наизусть: S = 1/2h * a , где S - это площадь, h - высота,
а - основание треугольника, к
которому проведена высота
Формула звучит так: площадь треугольника равна половине
произведения высоты на основание.
В нашем случае высота = 8, основание = 15 + 6 = 21
S = 1/2 * 8 * 21 = 84 (кв.ед.измерения).
В том, что отрезок 8 - это высота, убеждает нас значок угла, который показывает нам прямой угол.

29 декабря 2022 07:20

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Назовите еденицы измерения углов. что называют градусом?... СРОЧНО 40 Б Один из углов равнобедренного тупоугольного треугольника на 48° меньше другого. Найдите больший угол этого треугольника С решением... В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=84 и BC=BM . Найдите AH... Диагонали прямоугольника ABCD пересекаются в точке O. Найдите угол между диагоналями если угол ABO=40 градусов... Объясните, пожалуйста, как решать данную задачу: Две стороны треугольника равны 17 и 8 см, а косинус угла между ними равен (15)/(17). Найдите площадь...