1. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.2. В правильной четырехугольной пирамиде SABCD точка О - центр основания, S - вершина, SD = 15, AC = 24. Найдите длину отрезка SO.
3. Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на п.

1 ответ

Посмотреть ответы

DevAdmin

1685

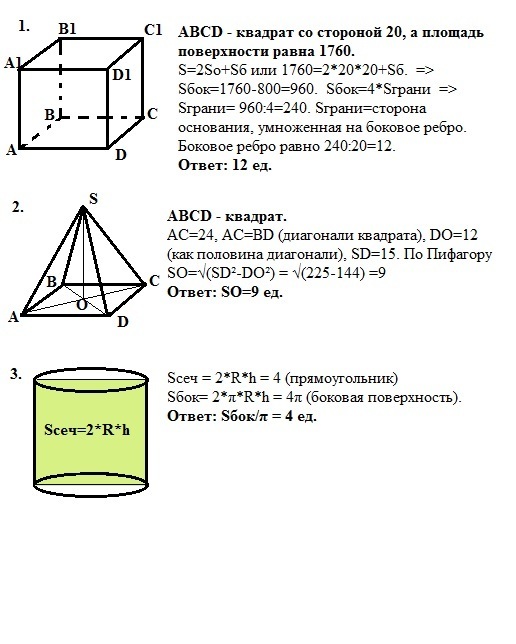
1. ABCD - квадрат со стороной 20, а площадь поверхности призмы равна 1760. Sп=2So+Sб или 1760=2*20*20+Sб. => Sбок=1760-800=960. Sбок=4*Sграни => Sграни= 960:4=240. Sграни=сторона основания, умноженная на боковое ребро. Боковое ребро равно 240:20=12.
Ответ: 12 ед.
2. ABCD - квадрат. АС=24, АС=BD (диагонали квадрата), DO=12 (как половина диагонали), SD=15. По Пифагору SO=√(SD²-DO²)=√(225-144) =√81 = 9 ед.
Ответ: SO=9 ед.
3. Sсеч = 2*R*h = 4 (прямоугольник). Sбок= 2*π*R*h = 4π (боковая поверхность).
Ответ: Sбок/π = 4 ед.

Хороший ответ

29 декабря 2022 07:24

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

ПОМОГИТЕ ПОЖАЛУЙСТА! Дана правильная четырехугольная пирамида SABCD с вершиной S стороны основания которой 6, а боковые ребра равны 12. Точка Е принад... ABCD-параллелограмм. Найдите BC. ПОМОГИТЕ ПОЖАЛУЙСТА ✌️... Какой из перечисленных путешественников исследовал внутренние районы Африки? 1) Дж. Кабот 2) Д. Ливингстон 3) А. Веспуччи 4) А. Макензи... Решить графически уравнение tgx=-корень из 3... Докажите, что если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны....