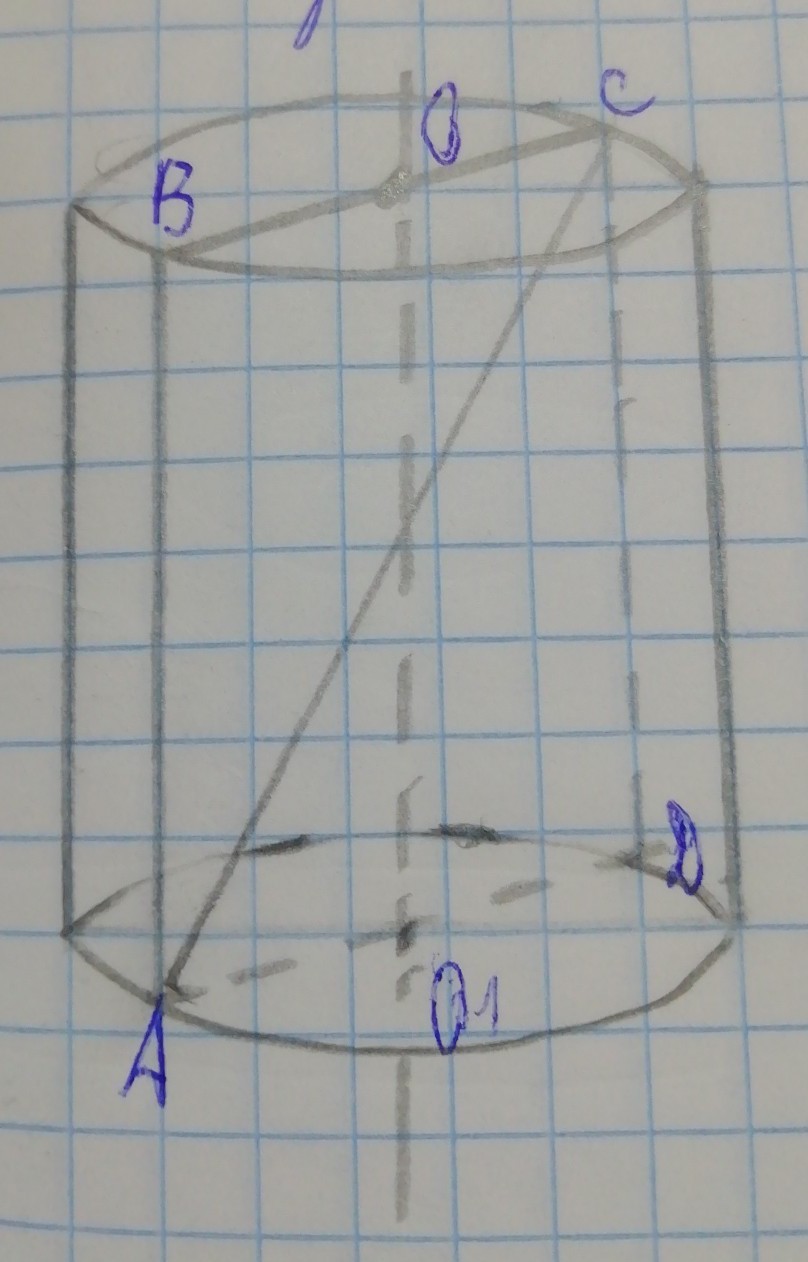
Осевое сечение цилиндра - квадрат, диагональ которого равна 20 см. Найдите высоту цилиндра и площадь основания цилиндра.

2 ответа

Посмотреть ответы

DevAdmin

1720

ΔАСD - прямоугольный, равнобедренный; АС=20 см по условию. Применим теорему Пифагора АD²+СD²=АС²; х²+х²=20²; 2х²=400; х²=200; х=√200=10√2. АD=СD=10√2 см. Высота цилиндра СD=10√2 см. Диаметр основания цилиндра равен АD=10√2 см. Радиус основания цилиндра равен R=(10√2)/2=5√2 см. Площадь основания цилиндра равна S=πR²=(5√2)²·π=50π см².

Хороший ответ

29 декабря 2022 11:34

Megamozg

2205

По условию АВСD - квадрат, Значит АD=СD . Пусть АD=СD=х.
ΔАСD - прямоугольный, равнобедренный; АС=20 см по условию. Применим теорему Пифагора АD²+СD²=АС²; х²+х²=20²; 2х²=400; х²=200; х=√200=10√2. АD=СD=10√2 см. Высота цилиндра СD=10√2 см. Диаметр основания цилиндра равен АD=10√2 см. Радиус основания цилиндра равен R=(10√2)/2=5√2 см. Площадь основания цилиндра равна S=πR²=(5√2)²·π=50π см².
Ответ: 10√2 см; 50π см

29 декабря 2022 11:34

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Здравствуйте ! Помогите , пожалуйста , решить задачу по геометрии ... Задача : отрезок АВ , изображённый на рисунке , параллелен стороне МР треугольни... Диагонали трапеции АВСD (AD¶BC) перпендикулярны. На основании АD выбрана точка К, такая что КВ=КD. Найти ВС, если АD=8, KD=7... Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырёхугольник A1 B1 C1 D2, вершинами которого являются середины отрезков OА, OВ... В прямоугольной трапеции ABCD (угол D=90 градусов) острый угол равен 30 градусов. Найдите угол AQN, образованный биссектрисами AM и CN углом А и С. Оч... Диагональ куба равна 6 см. Найти: а) ребро куба, б) косинус угла между диагональю куба и плоскостью одной из ее граней. Желательно с чертижем.....