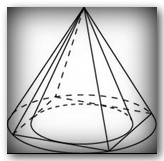
Во сколько раз объём конуса, описанного около правильной четырёхугольной пирамиды, больше объёма конуса, вписанного в эту пирамиду?

1 ответ

Посмотреть ответы

Megamozg

2205

Объём конуса равен трети произведения площади окружности-основания на высоту.
$V=\frac13SH=\frac13\pi RH$
Радиус основания описанного конуса равен $\frac{\sqrt2}2t$ , где t - сторона основания пирамиды (сторона квадрата).
Радиус основания вписанного конуса равен $\frac12t$ .
Тогда
$\frac=\frac{\frac13\pi\frac{\sqrt2}2t H}{\frac13\pi\frac12tH}=\sqrt2$
Объём описанного конуса больше объёма вписанного в $\sqrt2$ раз.

Хороший ответ

16 января 2023 21:56

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Какой результат вычисления функции f(x) = cos(2x) при x = 1?... Какие фразеологизмы используются в русском языке?... Если имеются два числа 0 и 2, то какой процент составляет число 2 от числа 0?... Помогите ещё решить пожалуйста.... Какое число является максимальным в задании?...