Основание пирамиды - равнобедренный треугольник с основанием, равным 12 см, и боковой стороной, равно 10 см. Вычислить высоту пирамиды, если все ее боковые грани образуют с плоскостью основания двугранные углы, равные 30 градусов.С чертежом.

2 ответа

Посмотреть ответы

Megamozg

2205

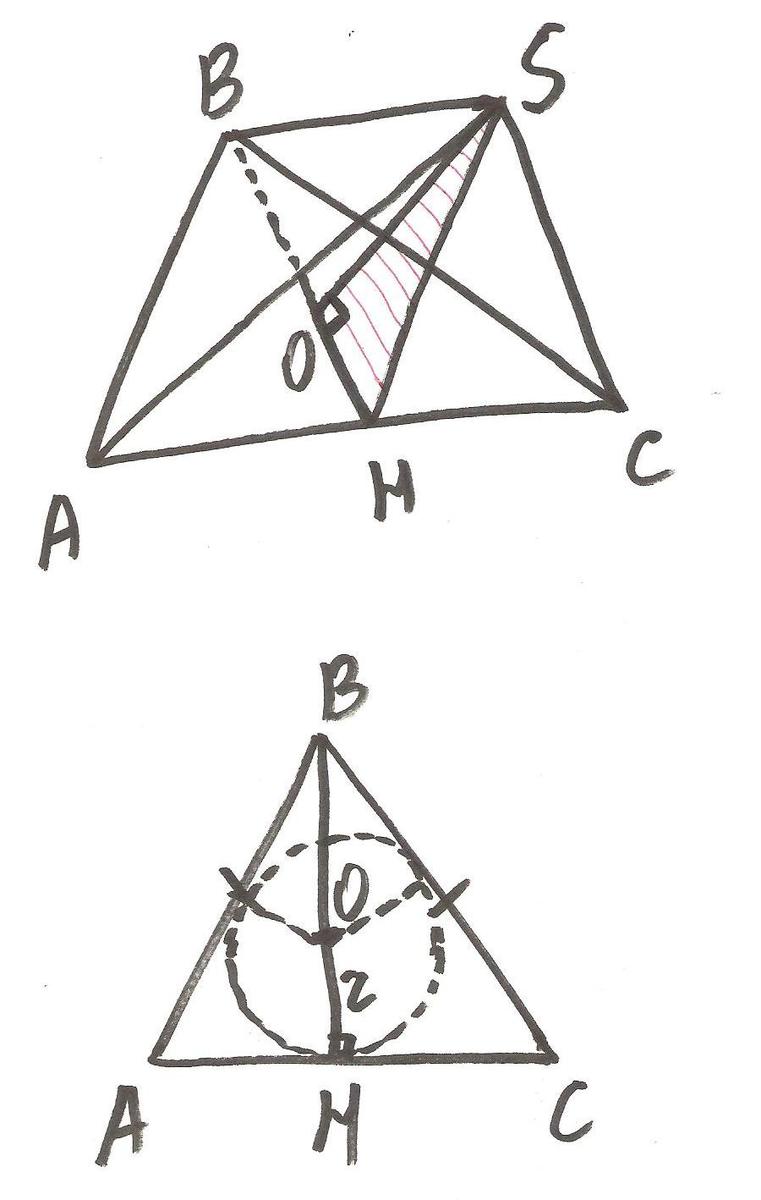
Дано: SABC - пирамида, АВ=ВС=10см, АС=12см, боковые грани образуют с основанием углы 30 градусов.
Найти: высоту SO.
Построение. К основанию треугольника АВС проведем высоту ВН, которая будет являться и медианой и биссектрисой, так как треугольник равнобедренный. Отрезок SH также является высотой, так как треугольник ASC равнобедренный. Значит, угол SHB - заданный в условии двугранный угол. Высота пирамиды проецируется на основание в точку О, являющуюся центром вписанной в треугольник АВС окружности, так как все грани пирамиды наклонены к основанию под одинаковым углом.
Решение: Рассмотрим прямоугольный треугольник OSH:
$\mathrm \angle SHO= \frac \Rightarrow SO=HO\cdot \mathrm \angle SHO$
Неизвестным остается отрезок НО, являющийся радиусом ранее упомянутой окружности.
Площадь треугольника равна половине произведения его основания на высоту, проведенную к основанию. С другой стороны площадь треугольника равна произведению его полупериметра на радиус вписанной окружности. Приравнивая эти площади, получим:
$\frac \cdot AC\cdot BH= \frac \cdot(AB+BC+AC) \cdot OH 
\\\
AC\cdot BH= (2AB+AC) \cdot OH 
\\\
OH= \frac$
BH найдем из треугольника АВН по теореме Пифагора, учитывая, что АН - половина АС.
$BH= \sqrt=\sqrt)^2 }
\\\
 BH= \sqrt)^2 }=8$
$OH= \frac=3$
$SO=3\cdot \mathrm 30^0=3\cdot \frac{ \sqrt } = \sqrt(sm)$
Ответ: $\sqrt$ см

Хороший ответ

16 января 2023 22:31

DevAdmin

1720

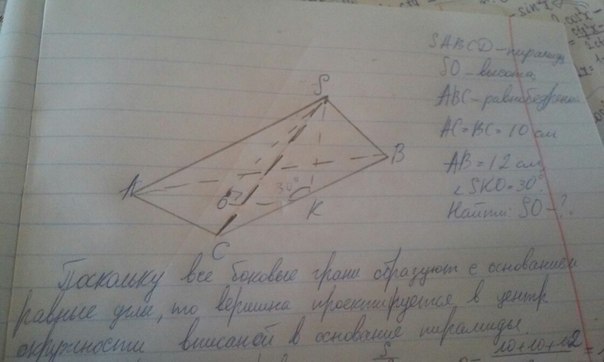
Чертеж в файле. Дальше не смотри
Поскольку все боковые грани образуют с основанием равные углы,то вершина проектируется в центр окружности вписаной в основание пирамиды.
S=pr. r=S/p
p=(AB+BC+AC)/2=16 (cm)
(S осн)²=p(p-AB)(p-BC)(p-AC)=16*6*6*4
Socн=48 см²
OK=r r=48/16=3(cm)
SO с треугольника SOK(O=90градусов)
tg30=OK/H
H=tg30/OK H= √3 (см)
Ответ: √3 см

16 января 2023 22:31

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

І. Какие фигуры называются равными? 2. Какие из фигур на рисунке 7 равны? 3 Какие из букв равны как геометрические фигуры? ... 1. В прямоугольном треугольнике DАS угол S равен 30°, угол А равен 90°. Найдите гипотенузу DS этого треугольника, если катет DА равен 8,5см.... отрезок AK - биссектриса треугольника CAE . Через точку K проведена прямая, параллельная стороне CA и пересекающая сторону AE в точке N. Найти углы тр... ав и ас касаются окружности В и С точки касания радиус 5 см угол ВАС=60 градусам Найти: АО АВ АС... Стороны основания прямоугольного параллелепипеда равны 3см и 5см, большая из диагоналей его боковых граней образует с плоскостью основания угол 60 гра...