Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
15 января 2023 02:18
1337
Задача,решите с пояснениями:Найдите углы,периметр и площадь треугольника,вершинами которого являются точки A(1;-1;3) ,B(3;-1;1), C(-1;1;3).Чисто ответы мне не нужны,у меня они есть-нужно решение и пояснение,Вам разве не нужно столько пкт?)
1
ответ
Найдём расстояния между точками, это и будут стороны треугольника.

Три точки всегда лежат только в одной плоскости, задача свелась к обычной планиметрии, мы знаем три стороны треугольника. Надо найти углы, периметр и площадь.

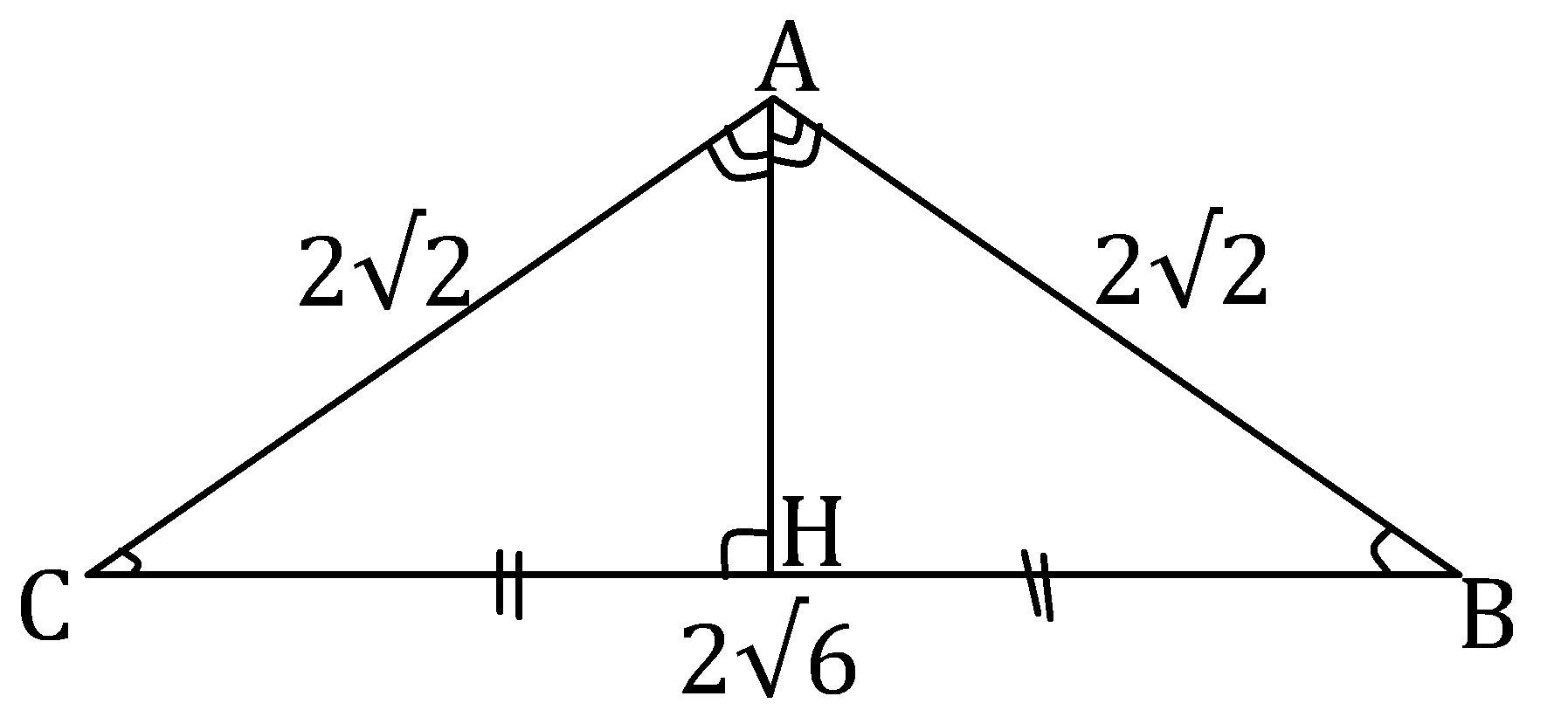
H∈BC; AH⊥BC; ΔABC - равнобедренный, поэтому высота будет и медианой, и биссектрисой.

В прямоугольном ΔAHC, катет AH в два раза меньше гипотенузы AC, поэтому угол лежащий напротив катета AH равен 30°, то есть ∠С = 30°.
∠B = ∠C = 30°. ∠A = 180° - 30° - 30° = 120°.
Ответ: ∠A = 120°; ∠B = 30°; ∠C = 30°;
Периметр: 2√2 · (2+√3);
Площадь: 2√3.
Три точки всегда лежат только в одной плоскости, задача свелась к обычной планиметрии, мы знаем три стороны треугольника. Надо найти углы, периметр и площадь.
H∈BC; AH⊥BC; ΔABC - равнобедренный, поэтому высота будет и медианой, и биссектрисой.
В прямоугольном ΔAHC, катет AH в два раза меньше гипотенузы AC, поэтому угол лежащий напротив катета AH равен 30°, то есть ∠С = 30°.
∠B = ∠C = 30°. ∠A = 180° - 30° - 30° = 120°.
Ответ: ∠A = 120°; ∠B = 30°; ∠C = 30°;
Периметр: 2√2 · (2+√3);
Площадь: 2√3.
0
·
Хороший ответ
17 января 2023 02:18
Остались вопросы?
Еще вопросы по категории Геометрия
В Выпуклом четырёхугольнике ABCD известно что угол ADC =60* и AB=AD=DC. Найдите угол ABD, если угол ВСА = 55...
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?...
Два катета прямоугольного треугольника равны 7 и 12.найдите его площадь...
Назовите все пары скрещивающихся ребер тетраэдра ABCD...
Какой будет рисунок у этой задачи? решать не нужно только рисунок Треугольник ABC и трапеция KMNP имеют общую среднюю линию EF, причем KP || MN, EF ||...