конус вписан в шар, диаметр основания конуса равен радиусу шара. объем конуса равен 6 найдите объем шара

1 ответ

Посмотреть ответы

Megamozg

2205

Подобные задачи чаще даются с радиусом конуса, равным радиусу шара.
Т.к. диаметр основания конуса равен радиусу шара, радиус основания конуса равен половине радиуса шара, т.е. R/2
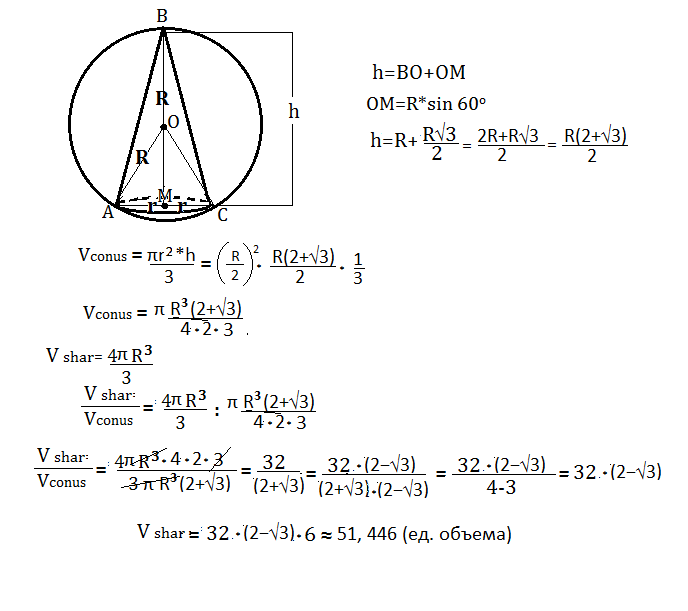
Высота конуса равна радиусу шара плюс высота правильного треугольника со сторонами, равными радиусу шара ( см. рисунок).
Формула объема шара
V=4πR³/3
Формула объема конуса
V=πr²h/3
1) Вычислим объем конуса, подставив в формулу радиус и высоту, выраженные через R.
2) Разделив выражение объема шара на найденный объем конуса, вычислим во сколько раз объем шара больше объема данного конуса.
3) Умножив 6 ( объем конуса) на число отношения объемов, получим объем шара.
Вычисления даны в приложении.
Результат:
объем шара равен 192*(2-√3) или ≈51,446 (ед. объема)

Хороший ответ

17 января 2023 02:53

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найдите углы ромба с диагоналями 2√3 и 2... Здравствуйте я Александр В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причем FC = 13 см. Найдите расстояние от точки F... Точки D (1; 4) и E (2; 2) — середины сторон AC и BC треугольника ABC соответственно. Чему равны координаты вершины C, если В (-3; -1)? *один правильн... Через концы отрезка AB и его середину M проведенны параллельные прямые, пересекающие некоторую плоскость в точках A1, B1, и M1. Найдите длиннуотрезка... В треугольнике ABC угол AСB равен 90, cos A = 0,8,AC = 4. Отрезок CH ― высота треугольника ABC. Найдите длину отрезка AH....