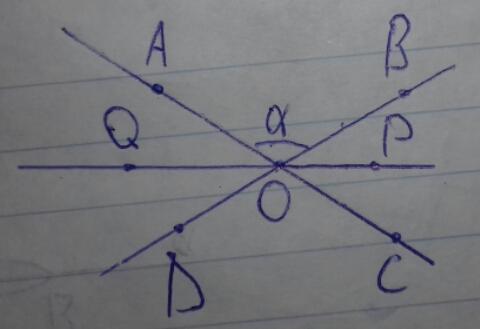
Докажите, что биссектрисы вертикальных углов лежат на одной прямой

1 ответ

Посмотреть ответы

Megamozg

2205

AC ∩ BD = O
Пусть ∠AOB=α, тогда ∠BOC=180°-α т.к. ∠AOB и ∠BOC смежные; так же ∠AOD=180° - α.
OP - биссектриса ∠BOC; OQ - биссектриса ∠AOD; ∠BOC и ∠AOD вертикальные.
∠BOP = ∠BOC÷2 = $\tt \dfrac -\alpha }2$ т.к. биссектриса делит угол пополам; так же ∠AOQ = ∠AOD÷2 = $\tt \dfrac -\alpha }2$
∠QOP = ∠AOQ+∠AOB+∠BOP = $\tt \dfrac -\alpha }2 +\alpha +\dfrac -\alpha }2 =\alpha +180^{\circ } -\alpha =180^{\circ }$
Значит ∠QOP развёрнутый ⇒ OQ,OP ⊂ QP. Доказано.

Хороший ответ

17 января 2023 03:06

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В какое озеро впадает 336 рек и вытекает одна... Докажите,что в равнобедренном треугольнике середина основания равноудалена от боковых сторон.... Луч ОС делит угол АОВ на два угла. найдите угол СОВ, если угол АОВ =78 градусов , а угол АОС на 18 градусов меньше угла ВОС.... Найдите синус,косинус и тангенс острых углов A и С прямоугольного треугольника ABC, если AC = 25см, AB = 7см.... Прямая, параллельная основаниям трапеции ABCD , пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF ,...