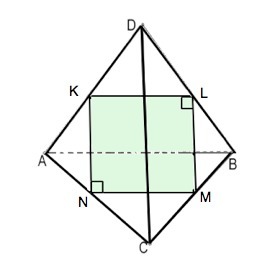
Ребра тетраэдра равны 38. Найдите площадь сечения, проходящего через середины четырех его ребер.

1 ответ

Посмотреть ответы

DevAdmin

1720

Ребра тетраэдра по условию равны, следовательно, он правильный и все его грани - правильные треугольники.
Каждая сторона сечения соединяет середины сторон такого треугольника и, как средняя линия соответствующей грани, равна половине параллельного ей ребра.
Скрещивающиеся ребра правильного тетраэдра перпендикулярны. DC⊥АВ⇒СD⊥MN, т.к. MN||АВ.
КN||CD⇒ KN⊥MN. Аналогично доказывается перпендикулярность всех соседних сторон сечения KLMN . Следовательно сечение- квадрат со стороной 38:2=19.
Площадь сечения 19²=361 (ед. площади)

Хороший ответ

17 января 2023 03:08

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В треугольнике ABC угол C равен 90°, CH - высота, угол A равен 44°. Найдите угол BCH. Ответ дайте в градусах.... Изучите свой школьный атлас. опишите виды географических карт. 5 класс география просвещение... Высота цилиндра равна 10 см. Площадь сечения цилиндра плоскостью, параллельной оси цилиндра и находящейся на расстоянии 6 см от нее, равна 160 см2. Вы... Прямоугольный параллелепипед у которого все рёбра ровны... Что такое длина отрезка...

Ребра тет­ра­эд­ра равны 38. Най­ди­те пло­щадь се­че­ния, про­хо­дя­ще­го через се­ре­ди­ны че­ты­рех его ребер.

Ребра тетраэдра равны 38. Найдите площадь сечения, проходящего через середины четырех его ребер.